Homothétie

[Anonyme]

Bonjour,

j'ai un petit problème pour un exercice de Maths que j'ai fait en interro mais dont j'ai pas trouvé la solution, si quelqu'un pouvait m'aider :

Soit ABCD un trapèze, O le point d'intersection de ses diagonales, et M un point extérieur à ce trapèze.
La parallèle à (AM) passant par C coupe la parallèle à (BM) passant par D en N.
On appelle h l'homothétie de centre O tel que h(A)=C.
Montrez que M, N et O sont alignés.

je ne vois pas du tout comment faire merci de m'aider

Rob'

[becirj]

Bonjour

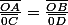
donc si h(A)=C alors h(B)=D.

L'image d'une droite par une homothétie est une droite parallèle donc :
- l'image de (AM) est la parallèle à (AM) passant par h(A)=C
- l'image de (BM) est la parallèle à (BM) passant par h(B)=D.

Le point d'intersection de (AM) et (BM) a pour image par h le point d'intersection de la parallèle à (AM) passant par C et de la parallèle à (BM) passant par D soit M a pour image N par h.

Un point et son iamage sont alignés avec le centre de l'homothétie donc les points O, M, N sont alignés.

[rene38]

Bonjour

On suppose que les bases du trapèze ABCD sont [AB] et [CD].
Par hypothèse, h est l'homothétie de centre O telle que h(A)=C.
Pas de problème pour montrer que h(B)=D (par exemple avec Thalès).
L'image d'une droite par une homothétie est une droite parallèle donc
h(AM) est la droite parallèle à (AM) et passant par h(A)=C : h(AM) = (CN)
De même h(BM) = (DN)
Donc l'image du point d'intersection de (AM) et (BM) est le point d'intersection de (CN) et (DN)
c'est à dire l'image de M est N : h(M) = N
Un point et son image sont alignés avec le centre de l'homothétie : M, N et O sont alignés.

Bonjour Becirj. Ex-aequo et pour dire la même chose !

[becirj]

Beau tir groupé !

[Anonyme]

Merci beaucoup, c'est vraiment sympa :)