Bonjour tout le monde,
je suis en seconde et je commence les fonctions affines.
Mais j'ai de gros problème sur les factorisation notamment
2x²-8x+6
Je n'y arrive vraiment pas :/
Si quelqu'un peut m'expliquer et me donner des petits exercices pour voir si j'ai compris ?
Factorisation
16 messages
- Page 1 sur 1
par gigamesh » 12 Mar 2010, 22:00
La fonction =2x^2-8x+6)
n'est pas affine (à cause du 
).
Pour la factorisation, appliques ton cours :
*plan A : on cherche un facteur commun
*plan B : on cherche des carrés pour utiliser une identité remarquable
Ici, = 2.x.x-2.2.2.x+2.3)
; les facteurs du premier terme sont 2, x et x, ceux du deuxième terme sont 2, 2, 2 et x, et ceux du troisième terme sont 2 et 3.
Le seul facteur qui soit commun aux trois termes est 2.
Donc=2(x^2-4x+3))
.
Bon, factoriser sert par exemple à utiliser la propriété "un produit est nul quand un facteur est nul" ; mais dire que résoudre
revient à résoudre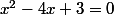 
ne nous avance guère, car l'équation est toujours du second degré (avec des ).
En fait, dans ce type d'exercice, factoriser signifie "factoriser le plus possible ", c'est-à-dire avec 3 facteurs plutôt que 2 si c'est possible.
C'est possible.
D'abord, il faut connaître ses identités remarquables.
Ensuite remarquer que
ça ressemble à un truc que du a du faire à peu près mille fois en troisième.
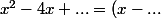^2)
Une fois que tu as complété ceci, tu remplaces par ^2-...)
et tu finis avec une autre identité remarquable.
=2(x^2-4x+3) = 2 ( (x-...)^2-... +3 ) = 2((x-...)^2-1) = ....)
Pour la factorisation, appliques ton cours :
*plan A : on cherche un facteur commun
*plan B : on cherche des carrés pour utiliser une identité remarquable
Ici,
Le seul facteur qui soit commun aux trois termes est 2.
Donc
Bon, factoriser sert par exemple à utiliser la propriété "un produit est nul quand un facteur est nul" ; mais dire que résoudre
En fait, dans ce type d'exercice, factoriser signifie "factoriser le plus possible ", c'est-à-dire avec 3 facteurs plutôt que 2 si c'est possible.
C'est possible.
D'abord, il faut connaître ses identités remarquables.
Ensuite remarquer que
Une fois que tu as complété ceci, tu remplaces
par Phil » 12 Mar 2010, 23:13
Bonsoir,
Une simple remarque x= 1 est racine évidente.... 2*1^2-8*1+6 =0
A partir de là: la factorisation est immédiate...
f(x) = 2(x-1)(x-3)
:id:
Avant de passer à la forme canonique, la première chose à faire, c'est d'abord de chercher les racines évidentes...
C'est tout
Bon courage
Phil
Une simple remarque x= 1 est racine évidente.... 2*1^2-8*1+6 =0
A partir de là: la factorisation est immédiate...
f(x) = 2(x-1)(x-3)
:id:
Avant de passer à la forme canonique, la première chose à faire, c'est d'abord de chercher les racines évidentes...
C'est tout
Bon courage
Phil
par absolut-diabolik » 13 Mar 2010, 07:01
Mais le délire de racine évidente , on connait pas ça en seconde.
par ceasars » 13 Mar 2010, 12:04
Je vous suis pas trop...
Sinon oui les racines évidentes on a pas vu.
Enfaite mon exo est :
Dans la figure ci dessous ABCD et BEFG sont des carrés. Déterminer les réels positives x tels que la somme des aires de ces deux carrées soit strictement supérieur a 10
AB=x
AE=4
et pour vous AE=AB+BE
avec ABCD sur la gauche de l'autre carré.
Pour les deux aires j'ai x²+(4-x)²>10
En développant j'ai 2x²-8x+16>10
J'ai mis le 10 de l'autre coté et voilà.
Je comptais aussi factoriser 2x²-8x+16 (avec les identités remarquables si on peux?)
puis mettre le 10 de l'autre coté pour avoir V10² soit a²-b²
Pour gigamesh
Veut tu dire x²-4x+...=(x-2)²??
Sinon oui les racines évidentes on a pas vu.
Enfaite mon exo est :
Dans la figure ci dessous ABCD et BEFG sont des carrés. Déterminer les réels positives x tels que la somme des aires de ces deux carrées soit strictement supérieur a 10
AB=x
AE=4
et pour vous AE=AB+BE
avec ABCD sur la gauche de l'autre carré.
Pour les deux aires j'ai x²+(4-x)²>10
En développant j'ai 2x²-8x+16>10
J'ai mis le 10 de l'autre coté et voilà.
Je comptais aussi factoriser 2x²-8x+16 (avec les identités remarquables si on peux?)
puis mettre le 10 de l'autre coté pour avoir V10² soit a²-b²
Pour gigamesh
Veut tu dire x²-4x+...=(x-2)²??
par gigamesh » 13 Mar 2010, 14:19
Veux tu dire x²-4x+...=(x-2)²??
C'est tout à fait ce que je veux dire ;
plus précisément, x²-4x+4=(x-2)² donc x²-4x=(x-2)² -4 (tu remarqueras que cette égalité est une identité, c'est-à-dire une égalité vraie pour n'importe quelle valeur de x).
Et du coup,
f(x)=2x²-8x+6 = 2(x²-4x+3)=2((x-2)²-4+3)=2((x-2)²-1)
f(x)=2( (x-1)² - 1² ) =2(x-2-1)(x-2+1) = 2(x-3)(x-1).
Ton inéquation est équivalent à 2x²-8x+6 > 0, en soustrayant 10 aux deux membres. Il n'est pas utile de factoriser avant d'avoir "tout mis à gauche", car après avoir "tout mis à gauche" on se retrouve avec gningningnin > 0 ce qui revient à étudier le signe de gningningnin ; et étudier un signe on sait faire, en particulier en factorisant et en écrivant le signe de caque facteur dans un tableau de signes.
C'est tout à fait ce que je veux dire ;
plus précisément, x²-4x+4=(x-2)² donc x²-4x=(x-2)² -4 (tu remarqueras que cette égalité est une identité, c'est-à-dire une égalité vraie pour n'importe quelle valeur de x).
Et du coup,
f(x)=2x²-8x+6 = 2(x²-4x+3)=2((x-2)²-4+3)=2((x-2)²-1)
f(x)=2( (x-1)² - 1² ) =2(x-2-1)(x-2+1) = 2(x-3)(x-1).
Ton inéquation est équivalent à 2x²-8x+6 > 0, en soustrayant 10 aux deux membres. Il n'est pas utile de factoriser avant d'avoir "tout mis à gauche", car après avoir "tout mis à gauche" on se retrouve avec gningningnin > 0 ce qui revient à étudier le signe de gningningnin ; et étudier un signe on sait faire, en particulier en factorisant et en écrivant le signe de caque facteur dans un tableau de signes.
par ceasars » 13 Mar 2010, 15:20
D'accord mais le tableau des signes aurait aussi permis de savoir les valeurs de x
pour les quels sa fait >10 non?
2(x-3)(x-1)>10
Comment faire ?
Désolé je suis nul ^^
pour les quels sa fait >10 non?
2(x-3)(x-1)>10
Comment faire ?
Désolé je suis nul ^^
par gigamesh » 13 Mar 2010, 21:42
Le nombre zéro est très spécial (beaucoup plus que le nombre 10).
Par exemple, si a0. Et de même pour les autres règles des signes que tu as vues en cinquième et quatrième. Attention quand même, si a0 et b>0 alors a+b>0, mais si a0 alors le signe de a+b peut être + ou -, ça dépend ; dans ce cas, on dit qu'on a une forme indéterminée ; p.ex -5+3=-20.
Pour les comparaisons à 10, il n'y a pas du tout ce genre de règles !
qq exemples :
* a=-12 10
* a =-4 10
Donc l'idée c'est de ramener toutes les équations que tu rencontres à la forme machin 0 ou bien machin
0 ou bien machin 
0 ; puis de factoriser (y compris le cas ou on met au même dénominateur) ; puis de faire un tableau de signes.
Je répète (je suis lourd, mais c'est vraiment la méthode numéro un en maths au lycée) : "on met tout à gauche, on factorise, on fait un tableau de signes". Tu le répètes 3 fois dans ta tête à chaque fois que tu rentres en cours de maths, et tu devrais avoir au moins 12 au bac !
Par exemple, si a0. Et de même pour les autres règles des signes que tu as vues en cinquième et quatrième. Attention quand même, si a0 et b>0 alors a+b>0, mais si a0 alors le signe de a+b peut être + ou -, ça dépend ; dans ce cas, on dit qu'on a une forme indéterminée ; p.ex -5+3=-20.
Pour les comparaisons à 10, il n'y a pas du tout ce genre de règles !
qq exemples :
* a=-12 10
* a =-4 10
Donc l'idée c'est de ramener toutes les équations que tu rencontres à la forme machin 0 ou bien machin
Je répète (je suis lourd, mais c'est vraiment la méthode numéro un en maths au lycée) : "on met tout à gauche, on factorise, on fait un tableau de signes". Tu le répètes 3 fois dans ta tête à chaque fois que tu rentres en cours de maths, et tu devrais avoir au moins 12 au bac !
par ceasars » 13 Mar 2010, 23:56
2(x-3)(x-1)>10
2(x-3)(x-1)-10>0
C'est sa ?
Mais je suis trop nul en factorisation^^
2(x-3)(x-1)-10>0
C'est sa ?
Mais je suis trop nul en factorisation^^
par ceasars » 14 Mar 2010, 11:56
Bonjour et re
f(x)=2x²-8x+6 = 2(x²-4x+3)=2((x-2)²-4+3)=2((x-2)²-1)
f(x)=2( (x-1)² - 1² ) =2(x-2-1)(x-2+1) = 2(x-3)(x-1).
= (2x-6)(x-1) je fais tableau de signes et voilà?
Mais n'utilise tu pas la forme canonique dans ton calcul ? car on a pas le droit
f(x)=2x²-8x+6 = 2(x²-4x+3)=2((x-2)²-4+3)=2((x-2)²-1)
f(x)=2( (x-1)² - 1² ) =2(x-2-1)(x-2+1) = 2(x-3)(x-1).
= (2x-6)(x-1) je fais tableau de signes et voilà?
Mais n'utilise tu pas la forme canonique dans ton calcul ? car on a pas le droit
par Phil » 14 Mar 2010, 23:39
Bonjour,
D'abord, pour répondre à "absolut-diabolik", le "délire des racines évidentes" ne s'apprend pas... Cela se voit du premier coup d'oeil et ne me dites pas que c'est compliqué de remplacer x par 1,2 ou 3 dans des expressions du 2nd degrés!
Et que faites vous pour factoriser des expressions du 3ème degré? (sans passer par les formules de Cardan et autres...) et du nième degré ?(je ne dis pas que ça marche à tous les coups, mais ça aide surtout dans les cas scolaires...)
C'est en tout cas le conseil que nous donnaient les professeurs à partir de la 3ème avant de s'aventurer dans de longs calculs (même s'ils sont justes)!
Ceci dit la procédure de "gigamesh" est parfaitement correct : on redémontre la forme canonique sans le dire et c'est très bien!
Enfin pour "ceasars": oui, il faut étudier le signe de 2(x-1)(x-3) et trouver les valeurs de x telles que cette expression est positive...
Autrement dit faire un tableau en 4 lignes :
x variant entre - infini et + infini
x-1 avec comme valeur particulière x=1
x-3 avec comme valeur partculière x= 3
et enfin la ligne résultat....
ATTENTION : l'expression 2(x-3)(x-1)>10 est fausse: c'est 2(x-3)(x-1)>0 car vous avez déjà intégrer le 10 dans votre expression (16-10 =6)
Cordialement
Phil
D'abord, pour répondre à "absolut-diabolik", le "délire des racines évidentes" ne s'apprend pas... Cela se voit du premier coup d'oeil et ne me dites pas que c'est compliqué de remplacer x par 1,2 ou 3 dans des expressions du 2nd degrés!
Et que faites vous pour factoriser des expressions du 3ème degré? (sans passer par les formules de Cardan et autres...) et du nième degré ?(je ne dis pas que ça marche à tous les coups, mais ça aide surtout dans les cas scolaires...)
C'est en tout cas le conseil que nous donnaient les professeurs à partir de la 3ème avant de s'aventurer dans de longs calculs (même s'ils sont justes)!
Ceci dit la procédure de "gigamesh" est parfaitement correct : on redémontre la forme canonique sans le dire et c'est très bien!
Enfin pour "ceasars": oui, il faut étudier le signe de 2(x-1)(x-3) et trouver les valeurs de x telles que cette expression est positive...
Autrement dit faire un tableau en 4 lignes :
x variant entre - infini et + infini
x-1 avec comme valeur particulière x=1
x-3 avec comme valeur partculière x= 3
et enfin la ligne résultat....
ATTENTION : l'expression 2(x-3)(x-1)>10 est fausse: c'est 2(x-3)(x-1)>0 car vous avez déjà intégrer le 10 dans votre expression (16-10 =6)
Cordialement
Phil
par ceasars » 15 Mar 2010, 17:23
Bonjour,
moi mon professeur de 3ème nous a toujours dit de ne jamais remplacer x même pour un début :D
Sinon je ne suis pas passer par la forme canonique car je n'ai pas le droit (seconde) mais comme je vous est dit dans l'exo d'avant on a prouver que x²-4x+3=(x-1)(x-3)
Donc j'ai fait 2(x²-4x+3) et remplacer x²-4x+3 puis fais 2(x-1)(x-3) =(2x-2)(x-3)
puis tableau de signes :)
moi mon professeur de 3ème nous a toujours dit de ne jamais remplacer x même pour un début :D
Sinon je ne suis pas passer par la forme canonique car je n'ai pas le droit (seconde) mais comme je vous est dit dans l'exo d'avant on a prouver que x²-4x+3=(x-1)(x-3)
Donc j'ai fait 2(x²-4x+3) et remplacer x²-4x+3 puis fais 2(x-1)(x-3) =(2x-2)(x-3)
puis tableau de signes :)
par Sylviel » 15 Mar 2010, 19:25
Il n'y a pas de forme canonique ici... Pour les racines évidentes il y a à mon avis quiproquo :
- chercher des racines ne s'apprend pas, c'est simple, il suffit de faire du calcul mental de base
- avoir l'idée d'en chercher et savoir qu'en faire, ça ça s'apprend... et ce n'est pas le cas en seconde !
J'essaie de faire une explication rapide :
si tu as x²-3x+2 à factoriser tu remarques que la fonction f:x->x²-3x+2 vaut 0 si x=1 (1 est racine de x²-3x+2). Qu'est-ce que cela signifie ? Et bien cela veut dire que ton polynome peut s'écrire :
(x-1)*... où les ... correspondent à un autre polynome. Pourquoi ? Parce que comme x²-3x+2 s'annule en 1 tu peux mettre en facteur un terme qui s'annule en 1. Et il ne reste plus qu'à trouver les ...
Puisque le plus haut monome est x² les ... n'ont qu'un x (pas de carré sinon tu aurais du x^3) du coup tu cherches a et b tel que
x²-3x+2 = (x-1)(ax+b)
a = 1 de manière évidente (coefficient de x² quand on développe le produit)
et on trouve facilement b=-2 (partie constante quand on développe).
Attention cette factorisation ne fonctionne que parce que l'on a des polynomes... Mais c'est bien pratique !
- chercher des racines ne s'apprend pas, c'est simple, il suffit de faire du calcul mental de base
- avoir l'idée d'en chercher et savoir qu'en faire, ça ça s'apprend... et ce n'est pas le cas en seconde !
J'essaie de faire une explication rapide :
si tu as x²-3x+2 à factoriser tu remarques que la fonction f:x->x²-3x+2 vaut 0 si x=1 (1 est racine de x²-3x+2). Qu'est-ce que cela signifie ? Et bien cela veut dire que ton polynome peut s'écrire :
(x-1)*... où les ... correspondent à un autre polynome. Pourquoi ? Parce que comme x²-3x+2 s'annule en 1 tu peux mettre en facteur un terme qui s'annule en 1. Et il ne reste plus qu'à trouver les ...
Puisque le plus haut monome est x² les ... n'ont qu'un x (pas de carré sinon tu aurais du x^3) du coup tu cherches a et b tel que
x²-3x+2 = (x-1)(ax+b)
a = 1 de manière évidente (coefficient de x² quand on développe le produit)
et on trouve facilement b=-2 (partie constante quand on développe).
Attention cette factorisation ne fonctionne que parce que l'on a des polynomes... Mais c'est bien pratique !
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
par ceasars » 15 Mar 2010, 19:50
Merci mais comme je l'ai dit c'est bon
Enfin voilà ce que j'ai fais
Exo 1)
Démontrer x²-4x+3=(x-2)²-1 (Fait)
En déduire la forme factoriser de x²-4x+3 -> (x-1)(x-3)
Exo 2)
Patati patata on arrive a 2x²-8x+16>10
2x²-8x+6>0
2(x²-4x+3)>0
2((x-1)(x-3))>0
2(x-1)(x-3)>0
(2x-2)(x-3)>
et le tour est jouer il me semble =D
Enfin voilà ce que j'ai fais
Exo 1)
Démontrer x²-4x+3=(x-2)²-1 (Fait)
En déduire la forme factoriser de x²-4x+3 -> (x-1)(x-3)
Exo 2)
Patati patata on arrive a 2x²-8x+16>10
2x²-8x+6>0
2(x²-4x+3)>0
2((x-1)(x-3))>0
2(x-1)(x-3)>0
(2x-2)(x-3)>
et le tour est jouer il me semble =D
par Phil » 15 Mar 2010, 23:18
:we: Bonjour,
Tout à fait d'accord avec Sylvie!
A noter qu'une fois qu'on a trouvé un racine d'un polynôme du 2nd degré,
l'autre racine se déduit immédiatement puisque leur produit donne le terme constant du polynôme...
Cordialement
Phil
Tout à fait d'accord avec Sylvie!
A noter qu'une fois qu'on a trouvé un racine d'un polynôme du 2nd degré,
l'autre racine se déduit immédiatement puisque leur produit donne le terme constant du polynôme...
Cordialement
Phil
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :