Convergence de séries

par **izzie** » 18 Fév 2010, 19:24

Bonjour à tous,

Je dois étudier la convergence de la série ;) (log(1+3n+7n²)/(n²+1) et là je bloque...

Merci d'avance pour votre aide.

par **ffpower** » 18 Fév 2010, 19:29

Regarde un équivalent de la suite en l'infini

par **izzie** » 18 Fév 2010, 19:56

Oui c'est ce que j'ai essayé, mais je suis pas trés à l'aise avec la fonction log en plus comme l'intérieur de la parenthèse du log ne tend pas vers zero en l'infini... j'y arrive vraiment pas...

par **girdav** » 18 Fév 2010, 20:00

Pronostic : converge ou diverge selon toi?

par **izzie** » 18 Fév 2010, 20:03

je dirais converge vers zero vu que le dénominateur de la fraction est un polynome du second degré et le numérateur une composée de log...

par **girdav** » 18 Fév 2010, 20:10

Oui, le terme général tend vers

ce qui est un bon début.
Maintenant est-ce que la série est à termes positifs?

par **izzie** » 18 Fév 2010, 20:15

il s'agit de carré donc je dirai que oui... Mais en fait il faudrait que je trouve un equivalent à l'infini du numérateur c'est ca..? j'avoues que je ne vois vraiment pas..

par **girdav** » 18 Fév 2010, 20:20

Ce n'est pas nécessaire si tu n'aimes pas les équivalents. Ici, on peut encore s'en passer sans trop de calculs supplémentaires.
La série est à terme positifs comme quotient de "trucs" positifs donc tu peux procéder ainsi :
-si tu penses que la série converge, majore le terme général par celui d'une série à termes positifs dont tu sais d'avance qu'elle converge,
-si tu penses que la série diverge, minore le terme général par celui d'une série à termes positifs dont tu sais qu'elle diverge.
Peu importe que la majoration n'aie pas lieu pour tout

: il suffit qu'elle aie lieu à partir d'un certain rang.

par **izzie** » 18 Fév 2010, 20:36

Comme je pense qu'elle converge je peux utiliser le fait que ln n<= à n et donc que ln (1+3n+7n²)<= à 1+3n+7n² ?(j'espere que je ne dit pas une grosse betise...)

par **girdav** » 18 Fév 2010, 20:38

La majoration est trop brutale : ce qui est à droite de l'inégalité est le terme général d'une série divergente.

par **izzie** » 18 Fév 2010, 20:41

Mais je vois pas par quoi d'autre majorer...

par **girdav** » 18 Fév 2010, 20:45

Tu es d'accord que

? Donc en passant tout ça au logarithme...

par **izzie** » 18 Fév 2010, 20:53

Oula je suis totalement perdue..
ca me donne donc log(1+3n+7n²)/(n²+1) <= log (10n²)/(n²+1)
<= 2log (10n)/(n²+1)
Mais là je fais quoi..?

par **girdav** » 18 Fév 2010, 21:00

On a que

donc en divisant par

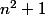
on a majoré le terme général par

.
Il reste à montrer que la série qui a pour terme général l'expression précédente converge, ce qui est plus facile que pour la série initiale.

par **izzie** » 18 Fév 2010, 21:13

Où vous avez écrit 10 ce ne serait pas plutôt 1 (log10=1)?
Si oui mon raisonnement serait :
Comme log n/ (n²+1) equivalent à log n / n² et que lim log n/ n^x =0 il reste que le terme 1/(n²+1) qui est equivalent a 1/n² or d'apres la série de riemann comme 2>1 la serie converge, c bien cela?

par **girdav** » 18 Fév 2010, 21:25

Je vais corriger le message.
On n'a pas l'équivalence que tu annonces (regarde la limite du quotient pour t'en convaincre) mais on peut écrire et éventuellement montrer que

pour

assez grand (la majoration continue).

par **izzie** » 18 Fév 2010, 21:34

Je ne comprends pas pourquoi mon equivalence est fausse..
logn/(n²+1) * n²/ log(n) = (n²logn (1)) / (n²logn (1+1/n²)) = 1/(1+1/n²) et ca ca tend vers un quand n tend vers l'infini ou est l'erreur?

par **mathelot** » 18 Fév 2010, 21:58

izzie a écrit:Bonjour à tous,

Je dois étudier la convergence de la série (log(1+3n+7n²)/(n²+1) et là je bloque...

Merci d'avance pour votre aide.

Bonsoir,

si on considère

qui n'est pas très éloigné de ln(n)
c'est (quasiment) le nombre de chiffres de l'entier n.

donc

a pour limite zéro . le terme général de ta série
est majoré par le terme général d'une série de Riemann convergente

Convergence de séries

convergence de séries

Qui est en ligne