Suites équiréparties et intégrale de Lebesgue
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
grandsaigne
- Messages: 3
- Enregistré le: 24 Jan 2010, 18:08
-
 par grandsaigne » 24 Jan 2010, 18:26
par grandsaigne » 24 Jan 2010, 18:26
Bonjour,
je me pose la question suivante : étant donnée une suite
u équirépartie sur un segment [a,b] de
R, on montre facilement que pour toute fonction
f continue :
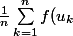 \rightarrow \frac{1}{b-a} \int_a^b f)
Est-ce aussi vrai pour une fonction intégrable au sens de Lebesque ?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 24 Jan 2010, 18:34
par Finrod » 24 Jan 2010, 18:34
En restant sur un compact il me semble que l'intégrabilité au sens de Lebesgue et de Riemann sont équivalentes.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Jan 2010, 18:36
par Doraki » 24 Jan 2010, 18:36
Pour des fonctions continues, oui.
-
grandsaigne
- Messages: 3
- Enregistré le: 24 Jan 2010, 18:08
-
 par grandsaigne » 24 Jan 2010, 18:37
par grandsaigne » 24 Jan 2010, 18:37
Pour des fonctions continues, oui. Mais est-ce vrai pour des fonctions Lebesgue-intégrables ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Jan 2010, 18:46
par Doraki » 24 Jan 2010, 18:46
Ah ben non, si tu prends la fonction caractéristique des irrationnels et que tu l'intègres avec une suite équi-répartie de rationnels sur [0;1], tu risques d'avoir des soucis.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités