Nombres complexes

par **tango38** » 21 Jan 2010, 18:41

Bonsoir à tous,

J'aimerai un peu d'aide pour un exercice de mathématique niveau terminale S ;

Voici l'énoncé :

"Résoudre dans C les équations d'inconnue z"
(je symbolise z avec une barre au dessus par z_)

a) 2z_ = i-1
b) (2z+1-i)(iz_+i-2)= 0
c) (z_-1)/(z_+1)= i

Et voici ce que j'ai trouvé :

a) 2z_ = (i-1)/2 = (1/2)-((1/2)i)

b) J'ai commencé à développer, mais je suis tombée sur un truc du genre 2i²zz_ , et je trouve ça un peu bizarre, est ce qu'il faut vraiment que je développe?

c) z_ = z_i + 2

Et pis dans l'énoncé, on me demande de résoudre les équations d'inconnue z (et pas d'inconnue z_), donc je pense que si je mets un résultat du style z_=, c'est considéré comme faux non ?

J'espère avoir été claire, merci d'avance! :)

par **Ericovitchi** » 21 Jan 2010, 18:48

oui on te demande z pas

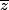
par contre si tu a trouvé

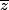
, il suffit de prendre le conjugué pour avoir z car

Pour b) c'est un produit de facteurs donc il ne faut surtout pas développer, il faut annuler chaque facteur.

par **tango38** » 21 Jan 2010, 19:09

Merci de m'aider si rapidement =)

a) je trouve alors z = (1/2) - ((1/2)i)

b) 'annuler les facteurs ?'
J'ai fait (iz_+i-2) = 1/(2z+1-i)

c) Et là j'ai obtenu z=2-iz_

par **Sa Majesté** » 21 Jan 2010, 20:43

tango38 a écrit:Merci de m'aider si rapidement =)

a) je trouve alors z = (1/2) - ((1/2)i)

Tu as fait une erreur de signe

tango38 a écrit:b) 'annuler les facteurs ?'
J'ai fait (iz_+i-2) = 1/(2z+1-i)

c) Et là j'ai obtenu z=2-iz_

Il faut trouver z = un nb complexe

Détaille tes calculs ...

par **Ericovitchi** » 21 Jan 2010, 20:49

non

--> z=-1/2 -i/2

Pour que le produit de facteurs soit nul (2z+1-i)(iz_+i-2)= 0
il faut que l'un ou l'autre des facteurs soit nul donc
soit

soit

il suffit de faire le produit en croix et de regrouper les

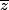
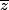
(1-i)=1+i, etc...

EDIT : Ha sa majesté dont c'était l'anniversaire hier m'a grillé ;+))

par **tango38** » 21 Jan 2010, 21:27

Ah oui, pour le a) j'ai fait une erreur de frappe, c'est bien

que je voulais dire ^^'

Ensuite pour le c), j'avais fait une erreur, à présent je trouve ;

(z_-1)/(z_+1) = i
z_-1 = i*(z_+1)
z_-1 = z_i+i
z_ = z_i+i+1

je bloque vraiment sur le b) qui est (2z+1-i)(iz_+i-2)=0

par **Teacher** » 21 Jan 2010, 21:34

J'y comprends rien !

par **tango38** » 21 Jan 2010, 21:41

Ben moi nan plus ..
Mais tu dis peut-etre ça à cause de la mauvaise présentation des calculs ?
J'arrive pas à mettre des barres sur les z, et puis en voulant mettre les fractions correctement ça enlevait des - ;)

par **Teacher** » 21 Jan 2010, 21:43

Oui c'est horrible cette présentation ___ ....
Si un produit est nul alors au moins l'un de ses facteurs est nul.

par **Teacher** » 21 Jan 2010, 21:51

C'est quoi ta réponse pour la a ?

par **Sa Majesté** » 21 Jan 2010, 21:57

tango38 a écrit:Ben moi nan plus ..
Mais tu dis peut-etre ça à cause de la mauvaise présentation des calculs ?
J'arrive pas à mettre des barres sur les z, et puis en voulant mettre les fractions correctement ça enlevait des -

Pour écrire

il faut taper [TEX) \large \frac{\bar{z}-1}{\bar{z}+1}= i[/TEX] en mettant un ] là où j'ai mis un )

par **tango38** » 21 Jan 2010, 21:57

Ah oui bien sûr !
J'ai trouvé, merci beaucoup =)

par **Sa Majesté** » 21 Jan 2010, 21:59

Ericovitchi a écrit:EDIT : Ha sa majesté dont c'était l'anniversaire hier m'a grillé ;+))

Perdu, c'était dimanche mais c'est l'intention qui compte ! :happy2:

Nombres complexes

Nombres complexes

Qui est en ligne