Suite et convergence

[Vilower]

Bonjour,

J'ai un exercice de Maths à faire et je bloque.
Soit (xn) une suite réelle.
a) Montrer que si (xn) converge, alors lim x2n - xn = 0
b) On pose Sn = Somme de k=1 à k=n de 1/k. (Sn) converge-t-elle ?

Voila.

Alors, pour la a, je pense à utiliser les suites extraites, où x2n serait une suite extraite de xn, au quel cas, elles auraient la même limite, et donc la différente d'une meme limite serait égale à 0. Mais je ne vois pas trop comment montrer que x2n est une suite extraite de xn. J'ai un peu de mal avec les suites extraites.

Et pour la b, je pensais à exprimer cette somme en une suite arithmétique, et ensuite exprimer la limite de cette suite. J'arrive à Sn = 0 + 1/n+1. Je sais que c'est faux, mais je n'arrive pas à traduire le fait que cela soit une somme en une suite.

Merci de votre aide :)

[girdav]

Salut.
Pour le a), on peut se servir de la définition d'une suite extraite pour montrer que en est une. Pour cela, quelle condition(s) doit satisfaire ?
Pour la b), je vais te surprendre: il faut se servir de a) en calculant .

[Vilower]

Phi doit être une application strictement croissante ..

Et pour la b, comment est-on sur que la réciproque fonctionne ?

[Doraki]

Je suis sûr que la réciproque fonctionne parceque c'est pas très dur de montrer que la suite S(2n)-S(n) = 1/(n+1) + 1/(n+2) + ... + 1/(n+n) ne peut pas converger vers 0.

[Vilower]

Je ne comprends pas pour la réciproque. Et je ne vois pas comment prouver que c'est une suite extraite.

[Finrod]

C'est une suite extraite par définition.

LA déf d'une suite extraite est qu'il existe une application croissante f de N dans N tel que

ici f est la multiplication par 2. Cela suffit comme argument.

Pour le b) le raisonnement se fait pas contraposé, cela signifie que tu vérifie que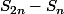 ne converge pas vers 0 ce qui implique que 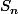ne peut pas converger.

(A implique B est équivalent à NON B implique NON A)

le terme réciproque est impropre.