Fonction
17 messages
- Page 1 sur 1
fonction
j'essaye de démontrer que l'équation 1+x+x²+x^3+....+x^(n-1)= x^n possède une unique solution sur ]0;+]
J'ai posé f(x)= 1+x+x²+x^3+....+x^(n-1)- x^n
f(0)=1 lim f= -x^n donc y'a au moins une solution
J'ai dérivé: 1+2x+3x²....+(n-1)x^(n-2) - nx^(n-1)
et je n'arrive pas à étudier le signe de la dérivé...
J'ai posé f(x)= 1+x+x²+x^3+....+x^(n-1)- x^n
f(0)=1 lim f= -x^n donc y'a au moins une solution
J'ai dérivé: 1+2x+3x²....+(n-1)x^(n-2) - nx^(n-1)
et je n'arrive pas à étudier le signe de la dérivé...
ah oui en faite il fallait bien utiliser cette expression
j'ai réussi à trouver f(x)= [(x^(n+1) -2x^n +1)/ (1-x)]
il me suffit donc d'étudier g(x)= x^(n+1)- 2x^n +1 comme tu l'as dit
g'(x)= (n+1)x^n -2nx^(n-1)
je me demande en fait si je ne peux pas faire un changement de variable en posant X=x^n mais est-ce que X² sera différent de x^(n+1)
j'ai réussi à trouver f(x)= [(x^(n+1) -2x^n +1)/ (1-x)]
il me suffit donc d'étudier g(x)= x^(n+1)- 2x^n +1 comme tu l'as dit
g'(x)= (n+1)x^n -2nx^(n-1)
je me demande en fait si je ne peux pas faire un changement de variable en posant X=x^n mais est-ce que X² sera différent de x^(n+1)
On fixe 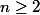 et on considère
et on considère \ :\ 1+x+x^2+x^3+....+x^{n-1}=x^n)
 n'est pas solution de
n'est pas solution de ) car
car  donc on a :
donc on a :
\ \Leftrightarrow\ \Big(x\not=1) et
et \ \Leftrightarrow\ \Big(x\not=1) et
et 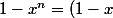x^n\Big))
 et
et )
Si on pose=x^{n+1}-2x^n+1) alors
alors =(n+1)x^n-2nx^{n-1}=(n+1)x^{n-1}\left(x-\frac{2n}{n+1}\right)) donc la fonction
donc la fonction  est décroissante sur
est décroissante sur  puis croissante sur
puis croissante sur  .
.
En utilisant le fait que=1>0) , que
, que =0) , que
, que  (ce qui prouve sans aucun calculs suplémentaires que
(ce qui prouve sans aucun calculs suplémentaires que <0) ) et que
) et que =+\infty) on voit que la fonction
on voit que la fonction  admet un seul zéro distinct de
admet un seul zéro distinct de  sur l'intervalle
sur l'intervalle  (il y a aussi un unique zéro strictement négatif lorsque
(il y a aussi un unique zéro strictement négatif lorsque  est pair)
est pair)
Questions :
1) Si on note ce zéro, quelle est la nature de la suite
ce zéro, quelle est la nature de la suite _{n\geq 2}) (monotonie, limite) ?
(monotonie, limite) ?
2) Peut-on donner le comportement assymptotique de la suite_{n\geq 2}) ?
?
Si on pose
En utilisant le fait que
Questions :
1) Si on note
2) Peut-on donner le comportement assymptotique de la suite
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si tu regarde bien ce que j'ai écrit, la solution x=1 n'est pas une solution de l'équation (E) : il n'y a donc bien qu'une seule solution à (E) (et la méthode de alavacommejetepousse le montre bien plus rapidement)
Effectivement, les questions que je pose sont uniquement pour "ceux qui veulent aller plus loin".
La convergence de la suite est façile à obtenir, sa monotonie est assez facile, mais un peu plus astucieux, et la recherche du comportement assymptotique commence à demander un peu de travail...
Effectivement, les questions que je pose sont uniquement pour "ceux qui veulent aller plus loin".
La convergence de la suite est façile à obtenir, sa monotonie est assez facile, mais un peu plus astucieux, et la recherche du comportement assymptotique commence à demander un peu de travail...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
ah oui c vrai
pour les questions en plus:
si on pose: fn(x)= x^(n+1)-2x^n+1
fn(x indice n)=0
f(n+1)(x indice n)= x^(n+2)-2x^(n+1)-1
= x(x^n+1-2x^n-1+1)-1
= x(fn(x indice n) +1)-1
=x-1
positive si x>1 et négative si x<1
donc f(n+1)(x indice n) > f(n)( x indice n) si x>1
non en faite je n'y arrive pas... Je peux avoir une piste?
pour les questions en plus:
si on pose: fn(x)= x^(n+1)-2x^n+1
fn(x indice n)=0
f(n+1)(x indice n)= x^(n+2)-2x^(n+1)-1
= x(x^n+1-2x^n-1+1)-1
= x(fn(x indice n) +1)-1
=x-1
positive si x>1 et négative si x<1
donc f(n+1)(x indice n) > f(n)( x indice n) si x>1
non en faite je n'y arrive pas... Je peux avoir une piste?
Tout ce que tu as écrit me semble parfaitement juste (et astucieux) pour montrer la croissance/décroissance de la suite _{n\geq 2}) .
.
Mais il faudrait commencer par du "plus simple" en trouvant un encadrement de (au vu du tableau de variation, c'est assez simple)...
(au vu du tableau de variation, c'est assez simple)...
Mais il faudrait commencer par du "plus simple" en trouvant un encadrement de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
