Convergence suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 17 Nov 2009, 17:51
par and1dx » 17 Nov 2009, 17:51
Bonjour voila le sujet:
Soit f une fonction continue sur [a; a], deux fois dérivables sur ] a; a[ telle que
 = 0)
et

bornée sur ] a; a[.
Montrer que la suite :
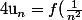+f(\frac{2}{n^2})+f(\frac{3}{n^2})+...+f(\frac{k}{n^2}))
converge et trouver sa limite
J'ai trouvé 0 mais je ne pense pas que ce soit ca....
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Nov 2009, 17:55
par girdav » 17 Nov 2009, 17:55
Salut.
Ce ne serait pas plutôt
})
?
Et quelle a été ta démarche?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 17 Nov 2009, 18:08
par Pythales » 17 Nov 2009, 18:08
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 17 Nov 2009, 18:44
par and1dx » 17 Nov 2009, 18:44
Non enfaite c'est
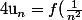+f(\frac{2}{n^2})+f(\frac{3}{n^2})+...+f(\frac{n}{n^2}))
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 17 Nov 2009, 18:50
par and1dx » 17 Nov 2009, 18:50
Pythales a écrit:Puisque
=0)
,
=\frac k{n^2}f'(0)+\frac{k^2}{2n^4}f"(c))
soit
}{n^2}\frac{n(n+1)}2+\frac{f"(c)}{2n^4}\frac{n(n+1)(2n+1)}6)
etc ...
Tu peux m'expliquer pourquoi
=\frac k{n^2}f'(0))
Merci

 par alavacommejetepousse » 17 Nov 2009, 18:57
par alavacommejetepousse » 17 Nov 2009, 18:57
Pythales a écrit:Puisque
=0)
,
=\frac k{n^2}f'(0)+\frac{k^2}{2n^4}f"(c))
soit
}{n^2}\frac{n(n+1)}2+\frac{f"(c)}{2n^4}\frac{n(n+1)(2n+1)}6)
etc ...
bonsoir
outch le c dépend de k on ne peut donc pas les regrouper
il faut s'en débarasser au contraire
-
Gomez150
- Messages: 1
- Enregistré le: 12 Aoû 2009, 10:59
-
 par Gomez150 » 17 Nov 2009, 20:43
par Gomez150 » 17 Nov 2009, 20:43
Bonjour silvouplait, expliqué moi CLAIREMENT , pourquoi Q n'est ni ouvert, ni fermé , svp , car le sylabus du prof est pa clair, je suis nouvo sur le forum je sais pas ou fo écrire les méssages, aidez moi svp
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 20:48
par Nightmare » 17 Nov 2009, 20:48
Gomez150 a écrit:Bonjour silvouplait, expliqué moi CLAIREMENT , pourquoi Q n'est ni ouvert, ni fermé , svp , car le sylabus du prof est pa clair, je suis nouvo sur le forum je sais pas ou fo écrire les méssages, aidez moi svp
Tu aurais dû créer un nouveau topic !
Q n'est pas fermé en particulier parce qu'il est dense dans R (on a donc des suites de rationnels qui tendent vers des irrationnels, Q n'est donc pas fermé).
Il n'est pas ouvert non plus car on ne peut trouver aucun intervalle ouvert contenu dans Q (puisqu'un intervalle ouvert contient au moins un irrationnel)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 17 Nov 2009, 20:59
par Pythales » 17 Nov 2009, 20:59
C'est vrai que

dépend de

mais comme
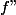
est borné, le dernier terme tend vers

La limite est facile à voir
 par alavacommejetepousse » 17 Nov 2009, 21:00
par alavacommejetepousse » 17 Nov 2009, 21:00
Pythales a écrit:C'est vrai que

dépend de

mais comme
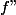
est borné, le dernier terme tend vers

La limite est facile à voir
certes mais bon
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités