Sommes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Watchmen
- Membre Naturel
- Messages: 26
- Enregistré le: 16 Sep 2009, 17:24
-
 par Watchmen » 27 Sep 2009, 09:08
par Watchmen » 27 Sep 2009, 09:08
Bonjour,
Je n'arrive pas à calculer plusieurs sommes en particulier celle-ci.
Sn = Somme pour i variant de 1 à n de la somme pour j variant de 1 à n de i+j.
Désolé je n'arrive pas à le taper en langage mathématique.
Merci.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 27 Sep 2009, 09:57
par fatal_error » 27 Sep 2009, 09:57
salut,
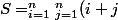\\<br />S = \left( \bigsum_{i=1}^n \bigsum_{j=1}^n i \right) + \left( \bigsum_{i=1}^n \bigsum_{j=1}^n j \right))
Notons
)
et
)

L'idée, c'est de déparer les sommes dans le cas de l'addition pour faire en sorte qu'on ait qqch qui ne dépend plus de l'indice et qu'on peut factoriser.
la vie est une fête

-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 27 Sep 2009, 10:09
par Pythales » 27 Sep 2009, 10:09
Je pense que le résultat est

A toi de détailler les calculs ...
-
Watchmen
- Membre Naturel
- Messages: 26
- Enregistré le: 16 Sep 2009, 17:24
-
 par Watchmen » 28 Sep 2009, 10:06
par Watchmen » 28 Sep 2009, 10:06
Okay merci c'est bon.
Par contre je bloque sur une autre somme :
;) 0;)2k;)n (n 2k) c'est le coefficient binomial 2k parmi n.
Il semble que ça fasse 2^(n-1) mais j'aimerais omettre une récurrence.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 28 Sep 2009, 13:39
par Finrod » 28 Sep 2009, 13:39
c'est le binome de newton
^{k})
= somme des

avec des valeurs de a et b bien choisis.
Donc,a moins que l'on te demande de refaire la preuve de ce truc, il te suffit de bien choisir a et b.
-
Watchmen
- Membre Naturel
- Messages: 26
- Enregistré le: 16 Sep 2009, 17:24
-
 par Watchmen » 28 Sep 2009, 16:55
par Watchmen » 28 Sep 2009, 16:55
Je vois pas comment faire apparaître le 2k, avec la somme du coefficient binomial (n k) ok mais là je ne vois pas.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 28 Sep 2009, 17:06
par Pythales » 28 Sep 2009, 17:06
-
Watchmen
- Membre Naturel
- Messages: 26
- Enregistré le: 16 Sep 2009, 17:24
-
 par Watchmen » 28 Sep 2009, 17:21
par Watchmen » 28 Sep 2009, 17:21
(1+1)^n + (1-1)^n = ;) (k=0 -> n) (n k) + 1
Je ne vois pas le lien
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 28 Sep 2009, 17:32
par Pythales » 28 Sep 2009, 17:32
Dévellope.
-
Watchmen
- Membre Naturel
- Messages: 26
- Enregistré le: 16 Sep 2009, 17:24
-
 par Watchmen » 28 Sep 2009, 17:41
par Watchmen » 28 Sep 2009, 17:41
Bah je ne vois pas quoi simplifier davantage mise à part que c'est 2^n + 1
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 28 Sep 2009, 18:16
par Pythales » 28 Sep 2009, 18:16
Je vais me faire tirer l'oreille par la modération si je te donne la solution.
Enfin ...
^n=C_n^0+C_n^1+C_n^2+C_n^3+...+C_n^n)
^n=C_n^0-C_n^1+C_n^2-C_n^3+...+(-1)^nC_n^n)
__________________________________

-
Watchmen
- Membre Naturel
- Messages: 26
- Enregistré le: 16 Sep 2009, 17:24
-
 par Watchmen » 28 Sep 2009, 19:23
par Watchmen » 28 Sep 2009, 19:23
D'accord pour les deux premières lignes mais je ne comprend pas la troisième.
Par contre si j'admet la dernière ligne il suffit en effet de diviser tout par deux pour tomber sur ce que l'on cherche.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
