bonsoir tout le monde j'ai un petit probleme
:mur: soit la fonction numerique f(x)=exp(x) +x-2
montrerf possed e un unique zero a tel que a appartienne [0,1]
on pose Uo=1
Un+1 ( n+1) en indce= Un -f(Un)/f'(Un). en etudiant la fonctio g telle que Un+1 =g(Un) montrer que poyur tout n dans N, Un >=a et que (Un) converge vers a.
je vous prie de mefournir un peu d'ade stp
Fonction numerique
3 messages
- Page 1 sur 1
Pour montrer que f(x) a un zéro unique le plus simple est d'étudier sa dérivée puis sa croissance et décroissance, montrer qu'elle est croissante entre 0 et 1 et que f(0) <0 et f(1) >0
ca montrera qu'il existe a tel que 0
Après, c'est la concrétisation de la méthode de newton pour approcher la solution
ca montrera qu'il existe a tel que 0
Après, c'est la concrétisation de la méthode de newton pour approcher la solution
bonsoir,
f est convexe et croissante, la courbe C_f est au dessus de ses tangentes,
les tangentes de la méthode de Newton , d'équation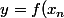+f'(x_n)(x-x_n) =l(x)) coupent donc l'axe x'ox
coupent donc l'axe x'ox
"avant" la courbe, ie,>0) si
si =0) donc
donc 
f est convexe et croissante, la courbe C_f est au dessus de ses tangentes,
les tangentes de la méthode de Newton , d'équation
"avant" la courbe, ie,
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
