Integrale double
19 messages
- Page 1 sur 1
integrale double
bonjours a tous
voila j'ai deux exercices pour lesquels j'ai des reponses finales mais pas de devellopement et je ne retombe evidemment pas sur la bonne solution
le premier c'est integrale de y=0 a y=racine de 3 de l'integrale de x=y/racine de 3 a y = 1 de x cube sur (x carré + y carré)
le deuxieme c'est: D est le disque de rayon a strictement superieur a 0 se tropuvant dans le premier quadrant et tangent aux axes de coordonnées. calculer I= double integrale (x,y) appartenant a D de (2a-x) ^(-1/2).
je suis desolée je suis une nouvelles dans maths forum donc je sais pas si il y a moyen d'ecrire les equations autrement qu'en toutes lettres....
voila j'ai deux exercices pour lesquels j'ai des reponses finales mais pas de devellopement et je ne retombe evidemment pas sur la bonne solution
le premier c'est integrale de y=0 a y=racine de 3 de l'integrale de x=y/racine de 3 a y = 1 de x cube sur (x carré + y carré)
le deuxieme c'est: D est le disque de rayon a strictement superieur a 0 se tropuvant dans le premier quadrant et tangent aux axes de coordonnées. calculer I= double integrale (x,y) appartenant a D de (2a-x) ^(-1/2).
je suis desolée je suis une nouvelles dans maths forum donc je sais pas si il y a moyen d'ecrire les equations autrement qu'en toutes lettres....
deja merci pour la traduction :++:
alors pour I1 je trouve r² * cos³ de phi que je sais integrer mais je n'arrive pas a trouver mes bornes d'integrations...
j'essaye en faisant r=x sur cos phi et je remplace par les deux bornes selon x mais alors je me retrouve avec un y que je veux remplacer par rsin phi mais alors mes r s'annule....
pour le I2 je passe a nouveau en coordonée polaire je pense que phi va de 0 a pi/2 mais pour r....j'ai l'impression que le cercle qui delimite le disque c'est (x-a)²+(y-a)²=a². je dois avouer que je me sents legerement perdue....
j'ai essayer de faire mes formules dans world pour simplifier les choses mais j'arrive pas a les importer.... :girl2:
alors pour I1 je trouve r² * cos³ de phi que je sais integrer mais je n'arrive pas a trouver mes bornes d'integrations...
j'essaye en faisant r=x sur cos phi et je remplace par les deux bornes selon x mais alors je me retrouve avec un y que je veux remplacer par rsin phi mais alors mes r s'annule....
pour le I2 je passe a nouveau en coordonée polaire je pense que phi va de 0 a pi/2 mais pour r....j'ai l'impression que le cercle qui delimite le disque c'est (x-a)²+(y-a)²=a². je dois avouer que je me sents legerement perdue....
j'ai essayer de faire mes formules dans world pour simplifier les choses mais j'arrive pas a les importer.... :girl2:
Je pense que ma 1ère suggestion n'est pas top lol
on va intégrer directement par rapport à y ensuite par rapport à x.
Donc il faudrait arranger l'expression de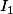
indice: à mettre en facteur au dénominateur
à mettre en facteur au dénominateur
Pour le domaine de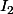 , c'est un disque ton r varie de 0 à a
, c'est un disque ton r varie de 0 à a  fallait pas oublier de hachurer le domaine.
fallait pas oublier de hachurer le domaine.
donc si on résume le domaine pour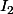
D={ }
}
Je pense que maintenant tu peux faire les calculs sans souci
on va intégrer directement par rapport à y ensuite par rapport à x.
Donc il faudrait arranger l'expression de
indice:
Pour le domaine de
donc si on résume le domaine pour
D={
Je pense que maintenant tu peux faire les calculs sans souci
Je pense que ma 1ère suggestion n'est pas top lol
on va intégrer directement par rapport à y ensuite par rapport à x.
Donc il faudrait arranger l'expression de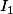
indice: à mettre en facteur au dénominateur
à mettre en facteur au dénominateur
Pour le domaine de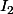 , c'est un disque ton r varie de 0 à a
, c'est un disque ton r varie de 0 à a  fallait pas oublier de hachurer le domaine.
fallait pas oublier de hachurer le domaine.
donc si on résume le domaine pour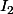
D={ }
}
Je pense que maintenant tu peux faire les calculs sans souci
on va intégrer directement par rapport à y ensuite par rapport à x.
Donc il faudrait arranger l'expression de
indice:
Pour le domaine de
donc si on résume le domaine pour
D={
Je pense que maintenant tu peux faire les calculs sans souci
ok merci a tous pour vos reponses :++:
pour I1 c'est bon mais pour I2
je fais 4*la double integrale de r(2a-rcosphi)^(-1/2)
pour r compris antre 0 et a et pour phi compris entre 0 et pi/2
mais voila j'arrive pas a integrer..... :hein:
et si je passe pas par les coordonnées polaires je me retrouve avec 2* l'integrale de [2a-(a²-y²)^(-1/2)]^(-1/2) pour y compris entre 0 et a....
je suis dsl j'ai un peu du mal :girl2:
pour I1 c'est bon mais pour I2
je fais 4*la double integrale de r(2a-rcosphi)^(-1/2)
pour r compris antre 0 et a et pour phi compris entre 0 et pi/2
mais voila j'arrive pas a integrer..... :hein:
et si je passe pas par les coordonnées polaires je me retrouve avec 2* l'integrale de [2a-(a²-y²)^(-1/2)]^(-1/2) pour y compris entre 0 et a....
je suis dsl j'ai un peu du mal :girl2:
finalement je comprends pas bien deja pourquoi x=a+phi*coteta et pas x=a*costeta pourquoi je pourrais pas resoudre mon integrale comme si mon disque etait centré sur l'origine pour teta compris entre 0et pi/2 et puis multiplier le resultat de la double integrale par 4
et surtout ce que je comprends pas du tout c'est pourquoi on peut dire que a=r pour moi a est une constante et r une variable....
et puis de toute maniere j'arive pas a faire l'integrale de (a-phicosteta)^-1/2 par rapport a teta....
et surtout ce que je comprends pas du tout c'est pourquoi on peut dire que a=r pour moi a est une constante et r une variable....
et puis de toute maniere j'arive pas a faire l'integrale de (a-phicosteta)^-1/2 par rapport a teta....
Pourquoi ne pas rester en coordonnées cartésiennes pour le calcul de I2 ?
Cela me semble presque immédiat.
Equation de la courbe délimitant le domaine: (x-a)²+(y-a)² = a²
y = a +/- V(a²-(x-a)²)
y = a +/- V(2ax-x²)
y = a +/- V(x(2a-x))
Et donc, sauf erreur, I2 peut s'écrire:
}}^{a+\sqrt{x(2a-x)}} dy)
Et cela, c'est sans difficultés...
:zen:
Cela me semble presque immédiat.
Equation de la courbe délimitant le domaine: (x-a)²+(y-a)² = a²
y = a +/- V(a²-(x-a)²)
y = a +/- V(2ax-x²)
y = a +/- V(x(2a-x))
Et donc, sauf erreur, I2 peut s'écrire:
Et cela, c'est sans difficultés...
:zen:
:lol2:
ouiiiiii!!!
j'ai essayer et je trouve effectivemment la reponse qu'il y a dans mon livre!!!
merci
Black Jack a écrit:Pourquoi ne pas rester en coordonnées cartésiennes pour le calcul de I2 ?
Cela me semble presque immédiat.
Equation de la courbe délimitant le domaine: (x-a)²+(y-a)² = a²
y = a +/- V(a²-(x-a)²)
y = a +/- V(2ax-x²)
y = a +/- V(x(2a-x))
Et donc, sauf erreur, I2 peut s'écrire:
Et cela, c'est sans difficultés...
:zen:
ouiiiiii!!!
j'ai essayer et je trouve effectivemment la reponse qu'il y a dans mon livre!!!
merci
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
