Asymptote

par **legrandchuck** » 04 Juin 2009, 17:07

Bonjour,

Je dois faire cet exercice mais je ne sais pas comment m'y prendre.

On donne la fonction

:

$:x$ "/>;)

où m est un paramètre réel.

On demande de déterminer la (les) valeur(s) de m telle(s) que

représente une asymptote horizontale.

Je sais que si on calcule la limite en plus et moins l'infini, on tombe sur

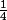
mais je ne vois pas bien comment déterminer

.

Merci d'avance.

par **Sve@r** » 04 Juin 2009, 17:31

Mes souvenirs sur les asymptotes sont loins (d'ailleurs j'ai jamais aimé ça)... mais une droite horizontale a un coefficient directeur de 0. Peut-être que ça peut aider...

par **Ericovitchi** » 04 Juin 2009, 17:32

non c'est une asymptote verticale que l'on cherche.
si tu cherches la limite pour x tendant vers l'infini, tu cherches une asymptote horizontale.

Une asymptote verticale c'est quand le dénominateur .... ?

par **legrandchuck** » 04 Juin 2009, 17:35

Non, c'est bien une horizontale.

par **Ericovitchi** » 04 Juin 2009, 17:52

ha oui pardon j'avais mal lu, c'est toi qui a raison.

Donc effectivement elle a une asymptote horizontale 1/4 quelque soit m

par **legrandchuck** » 04 Juin 2009, 17:57

Donc la valeur de

est R et c'est tout... C'est idiot comme exercice.

par **Ericovitchi** » 04 Juin 2009, 18:09

oui et à mon avis ils se sont trompé et la question était sur les asymptotes verticales. Ce qui te faisait regarder quand est-ce que le dénominateur de la fraction a des racines (car s'il a des racines alors il y a des asymptotes verticales). Tu calculais le discriminant et tu regardais quand est-ce qu'il était positif, négatif ou nul et tu en déduisais combien d'asymptotes verticales il y avait.

par **legrandchuck** » 04 Juin 2009, 18:34

Ok, donc pour calculer la racine, ça donne :

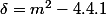
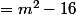
Mais après, je ne vois pas ce que je dois faire.

par **Ericovitchi** » 04 Juin 2009, 20:00

Pour qu'il y ait des racines, il faut que ce discriminant soit positif donc il faut étudier le signe de ce polynôme. un polynôme du second degré comme ça est du signe de a (c.a.d du coef de m^2) à l'extérieur des racines. Les deux racines sont faciles à trouver ; c'est 4 et -4.
Donc tu dis qu'à l'extérieur de ces racines il y a deux asymptotes, une seul quand on est sur une des deux racines et pas du tout quand on est au milieu.

par **legrandchuck** » 05 Juin 2009, 13:33

OK Il y a donc deux asymptotes ayant pour équation

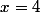
et

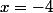
. Il y aura donc une asymptote si je remplace

par 4 OU par -4.

C'est bien ça?

par **Ericovitchi** » 05 Juin 2009, 16:37

non ça n'est pas ça. Tu confonds x et m.

Ton polynôme au dénominateur a un discriminant qui vaut

Il a deux racines quand

donc quand m 4
Mais les x des asymptotes sont variables et valent les racines du polynôme

c.a.d

et

donc ça n'est pas -4 et 4

par **legrandchuck** » 05 Juin 2009, 18:16

Ah oui. Merci, j'ai compris.

Asymptote

asymptote

Qui est en ligne