Intégration d'une fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jubo
- Messages: 6
- Enregistré le: 05 Avr 2009, 18:12
-
 par Jubo » 14 Mai 2009, 01:11
par Jubo » 14 Mai 2009, 01:11
Bonjour,
Je dois intégrer la fonction suivante, mais je n'ai aucune idée comment :
}{(exp(x)-1)^2} dx)
Pour ce qui est du 1/x^2, aucun problème. C'est plutôt pour l'exponentielle. Je n'es trouvé aucune identité intéressante. J'ai tenté de développer le carré et d'enlever les exp avec des log naturels, mais ça complique l'équation plutôt qu'autre chose. Je n'es pas tenté la technique des fractions partielles, mais je ne pense pas que ca puisse être utile.
Quelqu'un a t'il un début de chemin que je puisse prendre?
Merci d'avance :we:
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 14 Mai 2009, 06:23
par le_fabien » 14 Mai 2009, 06:23
Bonjour,
tu peux voir que l'expression est de la forme U'/U² avec U=e^(x)-1.
Une primitive est donc -1/U. :zen:
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 14 Mai 2009, 07:56
par Euler07 » 14 Mai 2009, 07:56
Niveau lycée les intégrales impropres ?
-
Jubo
- Messages: 6
- Enregistré le: 05 Avr 2009, 18:12
-
 par Jubo » 14 Mai 2009, 21:25
par Jubo » 14 Mai 2009, 21:25
Je suis étudiant au Québec, la plupart des mes cours s'apparentent au lycée, il se peut que certains des mes cours ne le soit pas, désolé!
Sinon, dans le fond, une fois le changement de variable fait, mon intégrale doit ressembler à :

Car si
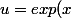-1)
alors
 = u + 1)
.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mai 2009, 21:30
par uztop » 14 Mai 2009, 21:30
Bonsoir,
en réalité Fabien ne te proposait pas de faire un changement de variable mais de calculer directement la primitive de la fonction qui est sous l'intégrale.
-
Jubo
- Messages: 6
- Enregistré le: 05 Avr 2009, 18:12
-
 par Jubo » 14 Mai 2009, 21:46
par Jubo » 14 Mai 2009, 21:46
Merci de ta réponse.
J'avoue être un peu perdu. Je comprends que la primitive est -1/u, s'il n'y avait rien en haut de la fraction. Mais là, je fais quoi du haut? Il doit y avoir juste un petit concept que j'arrive pas à saisir.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mai 2009, 21:55
par uztop » 14 Mai 2009, 21:55
non justement, quand tu dérives 1/u, tu obtiens

(u est une fonction)
Donc si tu dis que
 = e^x-1)
, ça donne quoi quand tu dérives 1/u ?
-
Jubo
- Messages: 6
- Enregistré le: 05 Avr 2009, 18:12
-
 par Jubo » 14 Mai 2009, 22:12
par Jubo » 14 Mai 2009, 22:12
Pour une raison que j'ignore, je ne connaissais pas le fait que la dérivée de 1/u où u est une fonction égale -u'/u². Moi tout ce que je pensais c'était que 1/u donne -1/u². Après une consultation sur Wikipédia, j'ai vu ceci et maintenant je comprends.
Merci beaucoup pour ton aide

Ps. Ca donne :
}{(exp(x)-1)^2})
soit exactement ce que je veux intégrer.
Edit: Merci, j'ai fait attention à la négation :++:
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mai 2009, 22:16
par uztop » 14 Mai 2009, 22:16
attention, tu oublies le signe -
La dérivée de 1/u est -u'/u²
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
