Une équation.

[Piccolo Rompicollo]

Bonjour à tous ! Est-ce que vous me pourriez résoudre un problème ?

Il faut démonter que l’équation possède au moins une racine complexe.

Merci !

[Nightmare]

Salut :happy3:

Essaye avec le théorème de Rouché en considérant et .

[yos]

As-tu essayé de poser z=x+iy ?

[Piccolo Rompicollo]

Oui, bien sûr. Mais alors la nécessité surgit d’analyser le système : et . Il me semble que c’est une question plus embrouillée.

D’un autre côté, l’image de l’application c’est un cercle, quand celui de c’est une droite. Ils peuvent avoir alors une ou deux points communs tels que . Qu’en pensez-vous ?

P.S. Pardon de mon français.

[fourize]

bonjour,

D’un autre côté, l’image de l’application c’est un cercle, quand celui de c’est une droite. Ils peuvent avoir alors une ou deux points communs tels que . Qu’en pensez-vous ?
P.S. Pardon de mon français.

effectivement, il devait avoir au moins une solution.
par contre je ne suis pas assez haut pour parler de théorème de Rouché mais
il m'a l'air convenable avec ce que j'avancerai un peu plus loin.
[url="http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Rouch%C3%A9"]voir ici le théorème de Rouché[/url]. si ça peut aider:-)

après moi ce que je te propose c'est de faire f(Z)= Z-
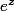
et faire un tableau de variation !!

PS. j'en suis pas sur qu'on etudie les fonctions complèxe comme dans IR mais si c'est le cas alors tout ira bien .

à bientot

[yos]

Oui, bien sûr. Mais alors la nécessité surgit d’analyser le système : et . Il me semble que c’est une question plus embrouillée.

Ca te donne le système
et , qui, par continuité, doit possèder une solution avec dans .

D’un autre côté, l’image de l’application c’est un cercle, quand celui de c’est une droite. Ils peuvent avoir alors une ou deux points communs tels que . Qu’en pensez-vous ?

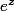
Non. L'image de est et l'image de est le plan complexe.

[Black Jack]

Par les log complexes.

z = |z|.e^(i.arg(z))

ln(z) = ln|z| + i.arg(z)

Et donc x + iy = ln|z| + i.arg(z)

On identifie les parties réelles et imaginaires des 2 membres et ...

Supposons x > 0 -->

x = ln|V(x²+y²)| et y = arctg(y/x)

On bidouille ces 2 équations et graphiquement par exemple ...

on arrive sauf erreur à :

z = 0,31817 + i.1,3372 est une solution. (valeurs approximatives pour x et y).

Il y en a d'autres ...

Mais une suffit pour l'énoncé.

Mais ce n'est peut-être pas ce qui était attendu ?

:zen:

[Piccolo Rompicollo]

Merci à tous de votre aide :++: Et surtout à yos

J’en suis venu à la conclusion qu’il est assez d’analyser la fonction avec . Et alors d’après le théorème de Bolzano-Cauchy nous avons au moins une résolution telle que car .

Quant aux images des applications. Je voulais dire que nous avons un circle et une droite si nous fixons la variable . Mais c’est pas grave maintenant