Exercice résolu
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Julia23
- Membre Relatif
- Messages: 139
- Enregistré le: 13 Sep 2007, 20:50
-
 par Julia23 » 25 Mar 2009, 21:49
par Julia23 » 25 Mar 2009, 21:49
Exercice résolu.
-
Sloan
- Membre Naturel
- Messages: 18
- Enregistré le: 25 Juin 2007, 23:35
-
 par Sloan » 25 Mar 2009, 22:06
par Sloan » 25 Mar 2009, 22:06
Bonsoir,
cos(pi/12+pi/12)=cos(pi/6)
...
C'est bon?
-
Julia23
- Membre Relatif
- Messages: 139
- Enregistré le: 13 Sep 2007, 20:50
-
 par Julia23 » 25 Mar 2009, 22:09
par Julia23 » 25 Mar 2009, 22:09
Oui mais ça c'est pour la question 1 non ?
Mais je ne sais pas faire la question deux ;) .
-
Sloan
- Membre Naturel
- Messages: 18
- Enregistré le: 25 Juin 2007, 23:35
-
 par Sloan » 25 Mar 2009, 22:11
par Sloan » 25 Mar 2009, 22:11
cos(2a)=cos(2pi/12)=cos(pi/6)
Et avec le dernier post et quelques formules de trigo...
-
Julia23
- Membre Relatif
- Messages: 139
- Enregistré le: 13 Sep 2007, 20:50
-
 par Julia23 » 25 Mar 2009, 22:14
par Julia23 » 25 Mar 2009, 22:14
Mais ce que je ne comprends pas, c'est pourquoi vous me rappelez la réponse que j'ai déja trouvé dans le 1 ? Car là c'est pour 2 pi/12. Alors que là on cherche pi/12 . La formule que l'on peut utiliser ici est
cos(2a) = 2cos²a-1 ?
-
Sloan
- Membre Naturel
- Messages: 18
- Enregistré le: 25 Juin 2007, 23:35
-
 par Sloan » 25 Mar 2009, 22:18
par Sloan » 25 Mar 2009, 22:18
a vaut pi/12, tu cherches cos(pi/12).
Dans la dernière formule que tu as cité, on peut voir apparaitre un cos²(a)...
Comme on connait la valeur de cos(2a)...
Tu vois la suite?
-
Julia23
- Membre Relatif
- Messages: 139
- Enregistré le: 13 Sep 2007, 20:50
-
 par Julia23 » 25 Mar 2009, 22:22
par Julia23 » 25 Mar 2009, 22:22
cos(2a) = 2cos²a-1
cos(pi/6) = 2 cos (pi/12)² - 1
(cos (pi/6) + 1)/2 = cos (pi/12)²
cos (pi/12) = racine carrée de ((cos (pi/6)+1)/2)
C'est ça ?
-
Sloan
- Membre Naturel
- Messages: 18
- Enregistré le: 25 Juin 2007, 23:35
-
 par Sloan » 25 Mar 2009, 22:31
par Sloan » 25 Mar 2009, 22:31
:p J'arrive pas bien à lire la réponse mais ca y ressemble. Tu dois pouvoir remplacer la valeur de cos(pi/6) que tu as calculé avant.
Tu peux faire le même raisonnement pour calculer cos(pi/8), sin(pi/8)...
-
Julia23
- Membre Relatif
- Messages: 139
- Enregistré le: 13 Sep 2007, 20:50
-
 par Julia23 » 25 Mar 2009, 22:33
par Julia23 » 25 Mar 2009, 22:33
cos (pi/12) = racine carrée de ((V3/2+1)/2)
Je crois qu'on y est là :) .
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 25 Mar 2009, 22:56
par oscar » 25 Mar 2009, 22:56
Bonsoir
Ce n' est pas la réponse définitive
cos² pi/12 = 1/ 4 (v3+2)= 1/16( 4v3+8) = 1/16 ( 5+2v12+2)=.(v6+v2)²/16
et cos pi/12 = (v6+v2)/4
 par busard_des_roseaux » 26 Mar 2009, 03:53
par busard_des_roseaux » 26 Mar 2009, 03:53
Bj,
}=\frac{sin 2x}{1+ cos 2x}) (***)
(***) =\frac{1 + cos 2x}{2})
 =\frac{1 - cos 2x}{2})
ou alors
amusant:
=\frac{sin x + cos x}{cos x - sin x})
puis
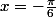
=\frac{ cos (\frac{\pi}{6})- sin(\frac{\pi}{6})}{cos (\frac{\pi}{6}) + sin(\frac{\pi}{6})}=\frac{\sqrt{3}-1}{sqrt{3}+1}) (***)
(***) donne
=\frac{1}{2+\sqrt{3}})
, les deux quantités sont égales à
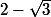
 par busard_des_roseaux » 26 Mar 2009, 08:44
par busard_des_roseaux » 26 Mar 2009, 08:44
oscar a écrit:cos pi/12 = (v6+v2)/4
évidemment, la formule d'Oscar est difficile à obtenir:
a priori, la trigonométrie donne:
=\frac{2+\sqrt{3}}{4})
mais , en utilisant
=cos a cos b + sin a sinb)
on obtient:
=\frac{1+\sqrt{3}}{2\sqrt{2}})
et donc l'expression trouvée précédemment était un carré parfait !
^2 = \frac{4+2\sqrt{3}}{8}=\frac{2+\sqrt{3}}{4})
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 26 Mar 2009, 12:00
par oscar » 26 Mar 2009, 12:00
Bjr
De toute façon on est amené à calculer V (2+v3)/4
C' est ce que j' ai fait
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
}=\frac{sin 2x}{1+ cos 2x}) (***)
(***) =\frac{1 + cos 2x}{2})
 =\frac{1 - cos 2x}{2})
=\frac{sin x + cos x}{cos x - sin x})
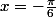
=\frac{ cos (\frac{\pi}{6})- sin(\frac{\pi}{6})}{cos (\frac{\pi}{6}) + sin(\frac{\pi}{6})}=\frac{\sqrt{3}-1}{sqrt{3}+1})
=\frac{1}{2+\sqrt{3}}) , les deux quantités sont égales à
, les deux quantités sont égales à