Espace de probabilité

[rafik]

bonjour,

Voila l'espérience : dans une boite il y a N=N1+N2+N3 jetons, N1 de couleur blanche, N2 noire, N3 rouge. On extrait simultanément k jetons avec k
Quel est l"espace de probabilité associé a cet expérience ?

moi je dis que oméga est une combinaison avec répetition (la répétition des couleurs) de k éléments parmi 3 (couleurs), mais je n'arrive pas à avoir la loi de probabilité!

MERCI

[yos]

L'espace de probabilité, c'est l'ensemble des issues possibles (c'est pas un nombre). Les issues sont ici les sous-ensembles de l'urne qui ont pour cardinal k. Il y en a où .
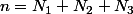
Quant à la loi sur cet univers, j'imagine qu'elle est uniforme.

[quinto]

Attention il n'y a pas nécessairement unicité de l'espace de probabilité, c'est toi qui décide ce que tu prends et qui décide la mesure que tu mets dessus pour mieux modéliser les expériences.

[Doraki]

Si les boules d'une même couleur sont indistingables, il faut regrouper des issues entre elles ; les nouvelles issues sont les partitions de k en a1+a2+a3 avec ai <= Ni.
Et sur cet univers-là, la loi n'est plus uniforme.

[yos]

Sans loi uniforme, on calcule pas.
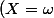D'où le choix que j'ai proposé. Ensuite on peut considérer une variable aléatoire X sur et regrouper ainsi certaines issues en des On obtient alors la nouvelle loi . Mais elle se calcule à partir de la loi uniforme P.