Exercice complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
novak
- Messages: 9
- Enregistré le: 02 Nov 2008, 20:05
-
 par novak » 14 Déc 2008, 14:37
par novak » 14 Déc 2008, 14:37
Bonjour,
Quelqu'un pourrait il m'expliquer comment calculer cos 5;) et sin 5;) en fonction de cos;) et sin;) ? Si possible en détaillant.
Merci d'avance
-
Sve@r
 par Sve@r » 14 Déc 2008, 14:40
par Sve@r » 14 Déc 2008, 14:40
Pas trop non (j'ai jamais trop aimé ces problèmes). Mais je pense qu'il doit y avoir dans ton cours des formules style cos(a+b) = ... ou cos(2a)=... etc. Il me semble que cela s'appelle "formules de Moivre" (à moins que je ne fasse une confusion)..
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Déc 2008, 14:45
par uztop » 14 Déc 2008, 14:45
Bonjour,
oui, mais il y a mieux à mon avis.
C'est une application de la formule d'Euler:
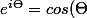+ i sin (\Theta))
)
est donc défini comme étant la partie réelle de

De la même façon,
)
est la partie réelle de

. On pourra remarquer que
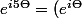^5)
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 14:48
par axiome » 14 Déc 2008, 14:48
Sve@r a écrit:Pas trop non (j'ai jamais trop aimé ces problèmes). Mais je pense qu'il doit y avoir dans ton cours des formules style cos(a+b) = ... ou cos(2a)=... etc. Il me semble que cela s'appelle "formules de Moivre" (à moins que je ne fasse une confusion)..
Tout à fait, il s'agit de la formule de Moivre qu'il faut utiliser :
+i*sin(\theta)]^n=cos(n\theta)+isin(n\theta))
où n est un entier naturel et

est un réel quelconque.
A noter que sous la notation exponentielle, cette formule devient complètement évidente, c'est d'ailleurs comme cela que je la retiens :
^n=e^{in\theta})
-
novak
- Messages: 9
- Enregistré le: 02 Nov 2008, 20:05
-
 par novak » 14 Déc 2008, 14:51
par novak » 14 Déc 2008, 14:51
hmm, b j'avais cru comprendre qu'il fallait utiliser le traingle de Pascal et ensuite mettre les réels d'un coté et les imaginaires de l'autre mais j'ai le résultat (qui est cos 5;)= cos^5;) - 10 cos3;) sin²;) + 5 cos;) sin^4;)) mais justement où sont les imaginaires?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Déc 2008, 15:24
par uztop » 14 Déc 2008, 15:24
comme l'a dit axiome, la formule de Moivre est assez évidente; ce que je te proposais revient exactement au même.
Il faut développer
+i.sin(\theta)]^5)
; la partie réelle donne les
)
et la partie imaginaire les
)
.
Est ce que tu peux détailler tes calculs? Je ne vois pas trop d'où vient ton résultat.
-
novak
- Messages: 9
- Enregistré le: 02 Nov 2008, 20:05
-
 par novak » 14 Déc 2008, 15:59
par novak » 14 Déc 2008, 15:59
En fait j'ai l'énnoncé et la correction d'où le résultat. Mais les étapes intermédiaires.. En fait ce que je ne comprend pas, c'est que l'on me demande de calculer cos 5;) en fonction de cos;) et je commence et termine avec des sinus..
ps: merci pour vos réponses.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Déc 2008, 16:08
par uztop » 14 Déc 2008, 16:08
est ce que tu as compris ce qu'on a écrit avant ? Les cos et les sin se calculent ensemble; il faut développer
+i.sin(\theta)]^5)
.
)
s'exprime en fonction de
)
ET de
)
(les deux sont nécessaires)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
