Nombres complexes

[Sarahh]

Bonjour je suis nouvelle ici donc pas encore très au point ne m'en voulez pas^^

Alors voilà je n'arrive pas une partie de mon dm j'espère que vous pourrez m'aider :

Soit A le point d'affixe 3i. On appelle f l'application qui, à tout point M d'affixe z, différent de A, associe le point M' d'affixe z'=(3iz-7)/(z-3i).

Soit z=x+iy et z'=x'+iy', sous forme algébrique.

a) Démontrer que pour z différent de 3i, on a x'=-16x/(x²+(y-3)²) et y'=3(x²+y²-(2/3)y-7)/(x²+(y-3)).

b) Déduire de a) l'ensemble Epsilon des points M du plan, distincts de A, pour lesquels z' est un imaginaire pur.

c) Déduire de a) l'ensemble Téta des points M du plan, distincts de A, pour lesquels z' est un réel.


Un grand merci à tous ceux qui m'aideront

[axiome]

Bonjour,
As-tu fais la question a) ?

[Sarahh]

non j'ai réussi aucune des trois questions :/

[axiome]

Bonjour je suis nouvelle ici donc pas encore très au point ne m'en voulez pas^^

Alors voilà je n'arrive pas une partie de mon dm j'espère que vous pourrez m'aider :

Soit A le point d'affixe 3i. On appelle f l'application qui, à tout point M d'affixe z, différent de A, associe le point M' d'affixe z'=(3iz-7)/(z-3i).

Soit z=x+iy et z'=x'+iy', sous forme algébrique.

a) Démontrer que pour z différent de 3i, on a x'=-16x/(x²+(y-3)²) et y'=3(x²+y²-(2/3)y-7)/(x²+(y-3)).

b) Déduire de a) l'ensemble Epsilon des points M du plan, distincts de A, pour lesquels z' est un imaginaire pur.

c) Déduire de a) l'ensemble Téta des points M du plan, distincts de A, pour lesquels z' est un réel.


Un grand merci à tous ceux qui m'aideront

Bon, ton exo, c'est surtout du calcul bête et méchant...

Pour la a), c'est tout simple : tu as z=x+iy
et
Il te suffit donc de remplacer les z de z' par x+iy et tu calcules pour arriver aux résultats donnés.
Bon courage. (pas mal de calculs...)

[Sarahh]

ok merci j'avais fait ça mais pas trouvé le bon résultat.. je vais réessayer et pour les questions b et c tu pourrais m'aider ?

[axiome]

Application du cours :
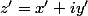
est un imaginaire pur
sa partie réelle x' est nulle : x'=0

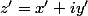
est un réel
sa partie imaginaire y' est nulle : y'=0

[Sarahh]

lol j'ai fait ça aussi au brouillon mais je bloque encore sur les calculs
Voilà ce que j'ai fait :

x'=0 donc -16x/(x²+(y-3)²)=0
donc -16x=0
donc x=0

y'=0 donc 3(x²+y²-(2/3)y-7)/(x²+(y-3)²)=0

x²+y²-(2/3)y-7=0

Et là je suis bloquée désolée si je suis assez pitoyable en calcul mais j'y arrive pas ! :/

[axiome]

x'=0 donc -16x/(x²+(y-3)²)=0
donc -16x=0
donc x=0

Tout à fait juste : tu as trouvé ton ensemble cherché :
C'est la droite d'équation x=0 (l'axe des ordonnées quoi)
Une petite rectification l'axe des ordonnées privé du point (0 ; 3).
En (0 ; 3), -16x/(x²+(y-3)²) n'est pas défini.

[axiome]

x²+y²-(2/3)y-7=0

Tu ne voudrais pas arranger cela de façon à avoir une équation de cercle ?

[Sarahh]

ah oui je crois avoir trouvé :

x²+y²-(2/3)y-7=0
x²+(y-1/3)²-1/9-7=0
x²+(y-1/3)²=8/3

:D

[Sarahh]

x²+(y-1/3)²=(8/3)² pardon :)

[Sarahh]

Par contre j'ai beau chercher la 3a je n'y arrive pas :S

En tout cas merci beaucoup pour ton aide.

[axiome]

x²+(y-1/3)²=(8/3)² pardon

Tout à fait juste.
Pour la 3a), pense à multiplier le dénominateur par le nombre conjugué de ce dénominateur.

[Sarahh]

J'ai essayé mais je bloque sur le conjugué de x+iy-3i je vois pas ce que ça pourrait être d'habitude on me demande le conjugué de x+iy.

[Sarahh]

up merci de m'aider^^