Continuité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
julien789
- Messages: 3
- Enregistré le: 01 Déc 2008, 19:44
-
 par julien789 » 01 Déc 2008, 19:49
par julien789 » 01 Déc 2008, 19:49
Bonjour,
Voici une étape que j'ai du mal à comprendre. Y'aurait-il quelqu'un pour m'éclairer ?
Considérons V et W espaces de Banach et (Tn) suite de L(V;W)
On pose Xn={ v de V tels que pour tout m naturel, ||Tm(v)|| < n }
On souhaite montrer que Xn est fermé et que l'union des Xn est V.
Pourquoi la continuité de Tm pour tout m suffit à assurer la fermeture de Xn ?
Merci d'avance
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Déc 2008, 19:53
par ThSQ » 01 Déc 2008, 19:53
C'est pas plutôt

plutôt que
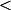
?
-
julien789
- Messages: 3
- Enregistré le: 01 Déc 2008, 19:44
-
 par julien789 » 01 Déc 2008, 19:58
par julien789 » 01 Déc 2008, 19:58
Oui, effectivement... Que cela change-t-il ?
(Je suis vraiment perdu sur ce problème, ça fait un bout de temps que je n'ai pas touché à l'analyse)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Déc 2008, 20:01
par ThSQ » 01 Déc 2008, 20:01
julien789 a écrit:Que cela change-t-il ?
Tout ....
-
julien789
- Messages: 3
- Enregistré le: 01 Déc 2008, 19:44
-
 par julien789 » 01 Déc 2008, 20:08
par julien789 » 01 Déc 2008, 20:08
Je ne suis pas sur de bien voir la chose en fait...
Qu'est-ce que la continuité fait la dedans ?
L'inégalité large donne directement un fermé ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 01 Déc 2008, 20:28
par Joker62 » 01 Déc 2008, 20:28
Image réciproque d'un fermé par une fonction continue pardis.
D'où l'importance de la possible égalité.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
