bonjour, svp pouvez vous m'aider à faire mon exercice ?
on considère la fonction numérique f définie sur R par f(x)=t - 3 e^3t-3 et sa courbe représentatrice C dans un repère orthogonal (unités graphique 5cm en absicce et 10 cm en ordonnée)
1/ étudier les limites de la fonction f en + et - l'infini
2/ montrez que la courbe C admet une asymptote oblique D dont on donnera une équation. Préciser la positionde C par rapport à la droite D.
3/ a) Déterminer la fonction dérivée f' d ela fonction
b) Résoudre l'équation, d'inconnue rélles t, f'(t)=0: on donnera la valeur exacte de la solution puis sa valeur arrondie au centième.
c) Etudier le sens de variation de la fonction f' et établir son tableau de variation.
d) Déterminer une équation de la tangente Tà la courbe C en son point d'abscisse 1.
e) Tracer les droites D et T et la courbe C dans le repère donné.
Merci d'avance de m'aider
Fonction expo
11 messages
- Page 1 sur 1
1. En - , il n'y a pas de forme indéterminée, tu devrais trouver.
, il n'y a pas de forme indéterminée, tu devrais trouver.
En + , on a une forme indéterminée
, on a une forme indéterminée =t(1-3\frac {e^{3t-3}}{t})) .
.
En utilisant les croissances comparées donc
donc =-\infty)
(Peut-être faut-il détailler davantage ! que damande ton professeur ?)
2.-t=-3e^{3t-3}) .
. donc en - l'infini C admet pour asymptote la droite d'équation y=x.
donc en - l'infini C admet pour asymptote la droite d'équation y=x.
-t=-3e^{3t-3}<0) donc la courbe C est en dessous de l'asymptote.
donc la courbe C est en dessous de l'asymptote.
3.a)=1-3\times 3 e^{3t-3}=1-9e^{3t-3})
b) f'(t)=0 lorsque



c) Je te laisse étudier le signe de f'(t) et faire le tableau de variation.
d)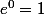 ,
, = 1-3e^0=-2) ,
, =1-9e^0=-8)
la tangente a donc pour équation-2=-8x+6)
En +
En utilisant les croissances comparées
(Peut-être faut-il détailler davantage ! que damande ton professeur ?)
2.
3.a)
b) f'(t)=0 lorsque
c) Je te laisse étudier le signe de f'(t) et faire le tableau de variation.
d)
la tangente a donc pour équation
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
