Je m'adresse à vous pour de l'aide sur un devoir maison de maths. Je tiens à préciser que j'ai de grosses lacunes en maths, donc si je fais des erreurs veuillez m'excuser :lol3:
Voici l'intitulé de l'exercice.
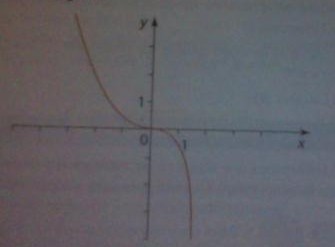
On considère la fonction numérique f définie et dérivable sur R telle que pour tout réel x on ait : f(x)=(x²/2)-x²e^x-1 . On note f' sa fonction dérivée. Le graphique ci-après est la courbe représentative de cette fonction telle que l'affichage d'une calcultratice dans un repère orthogonal. (Le graphique est ci-dessus)
1) Quelle conjecture pourrait-on faire concernant le sens de variation de sur l'intervalle [-3;2] en observant cette courbe ?
J'ai répondu : Il semblerait que sur l'intervalle [-3;2], la courbe représentative de la fonction f soit décroissante, et passe par l'origine.
Dans la suite du problème, on va s'intéresser à la validité de cette conjecture.
2) Calculez f'(x) et vérifiez que f'(x) =xg(x) où g(x)=1-(x+2)e^x-1
La ça coince déjà pour moi!
J'ai répondu : on sait que f(x) = (x²/2)-x²e^x-1 et que f est dérivable pour tout X sur [-3;2] par la forme W-U*V
D'où F' = W'-U'*V'
W = x^2/2 et W' = 2x/2 ( je suis pas sûr de celà)
U= -x² d'où U' = -2x
et V = e^x-1 et donc de la forme e^Z et E^z' = Z' *E^x-1 d'où V' = x*e^x-1
Si vous pouvez déjà m'aider à me corriger pour cela et m'aider à trouver une eventuelle formule ( si j'ai faux ^^) s'il vous plait
3) Etude du signe de g(x) suivant les variations de x
a) Calculez g'(x) et étudiez son signe suivant les valeurs du nombre réel x
b) En déduire le sens de variation de la fonction g, puis dressez son tableau de variation
c) Montrez que l'équation g(x)=0 possède une unique solution dans R. On note a(alpha) cette solution. Justifiez que 0.20<alpha<0.21
d) Déterminez le signe de g(x) suivant les valeurs de x
4) Sens de variation de la fonction f
a) Etudiez le signe de f'(x) suivant les valeurs de x
b) En déduire le sens de variation de la fonction f
c) Que pensez-vous de la conjecture de la question 1 ?
Voila merci par avance, mais sachant que je bloque au début je n'ai pas pu continué, mais je pense que je serai capable de réaliser la suite..Cependant si je galère, je referai peut être appel à vous si ça ne dérange pas.
Merci!
