Merci de m'aider à resoudre cet exo:
Etudier le prolongement par continuité des fct suivantes:
1)
2)
3)
Merci :hein:
Prolongement par continuité
12 messages
- Page 1 sur 1
Prolongement par continuité
par mathgaussmath » 20 Oct 2008, 13:42
Bonjour,
Merci de m'aider à resoudre cet exo:
Etudier le prolongement par continuité des fct suivantes:
1)=\frac{\sqrt{x+1}-\sqrt{x}}{\sqrt{x}}$)
, en 0.
2)=(exp(x)+2x)^{\frac{1}{x}}$)
3)=(1+\frac{5}{3x^2})^{x^2}$)
Merci :hein:
Merci de m'aider à resoudre cet exo:
Etudier le prolongement par continuité des fct suivantes:
1)
2)
3)
Merci :hein:
par nyafai » 20 Oct 2008, 14:17
Pour ça il te faut à chaque fois trouver le domaine de définition et calculer la limite des fonctions vers les points (non infini) pour lesquels la fonction n'est pas définie. Si cette limite est finie, la fonction est prolongeable par continuité en ce point.
Je te laisse trouver les intervalles de définition
Reste à calculer les limites. Dans les trois cas 0 est un point sur lequel la fonction n'est pas définie et pour lequel il faut calculer la limite.
1) il faut simplifier par
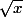
pour x>0
2) il faut écrire^{b(x)}=e^{b(x)ln(a(x))})
(en vérifiant bien que a(x) est positif sur le domaine de définition) et utiliser : }{u}=1)
dans la puissance
3) idem pour la réécriture mais il faut utiliser}{u}=0)
Je te laisse trouver les intervalles de définition
Reste à calculer les limites. Dans les trois cas 0 est un point sur lequel la fonction n'est pas définie et pour lequel il faut calculer la limite.
1) il faut simplifier par
2) il faut écrire
3) idem pour la réécriture mais il faut utiliser
Urgent
par mathgaussmath » 21 Oct 2008, 23:29
Bonsoir,
Je ne sais pas comment trouver le domaine de définition de + 2x)^{\frac{1}{x}}$)
???
Je ne sais pas comment trouver le domaine de définition de
par leon1789 » 22 Oct 2008, 08:37
mathgaussmath a écrit:Bonsoir,
Je ne sais pas comment trouver le domaine de définition de
Quelle est la définition de
je veux dire, comment calcule-t-on l'image de
Résolution d'une inéquation
par mathgaussmath » 23 Oct 2008, 11:11
Bonjour,
Je sais que: +2x)^{\frac{1}{x}}= exp(\frac{1}{x}ln(e^x+2x))
, le problème pour moi est de trouver les x qui vérifient 
?? le reste est facile je pense...
Je sais que:
par nyafai » 23 Oct 2008, 12:33
en dérivant 
tu obtiens quelque chose de strictement positif, donc 
est strictement croissante sur R, positive en x=0 et tend vers -infini en -infini. il existe donc 
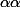
. d'où ton domaine de définition : 
par leon1789 » 23 Oct 2008, 12:35
mathgaussmath a écrit:Bonjour,
Je sais que:
oui, c'est exactement la définition et c'est aussi la bonne question.
La fonction x -> e^x+2x est croissante, et s'annule qu'une seule fois sur R.
Notons
Ta question est de savoir si on peut prolonger
par leon1789 » 23 Oct 2008, 12:36
nyafai a écrit:. d'où ton domaine de définition : ]
[
juste une coquille (en rouge).
par mathgaussmath » 25 Oct 2008, 23:09
alors, là je comprend qu'en utilisant le théorème des valeurs intermediaires, on pourrait en deduire l'existence de 
.
Maintenant, je trouve en fait que}=0)
?
En effet, voici comment j'ai fait:
}=lim_{x\rightarrow x_0} e^{\frac{1}{x}ln(e^x(1+2xe^{-x})})
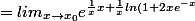}=e^1e^{\frac{-\infty}{x_0}}=0)
.
Donc f est prolongeable par continuité en x_0...
:++: ou :--:
Maintenant, je trouve en fait que
En effet, voici comment j'ai fait:
Donc f est prolongeable par continuité en x_0...
:++: ou :--:
par nyafai » 27 Oct 2008, 10:34
:--: il te manque juste de remarquer que est négatif, donc ta dernière limite est fausse et ca tend vers 
donc ce n'est pas prolongeable par continuité
par mathgaussmath » 27 Oct 2008, 11:18
:cry: Oui, t'as raison, j'ai pas fait attention que x_0 est négatif: et ça change beaucoup :ptdr:
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :