Titre non conforme - Attention !!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Alicouu
- Messages: 7
- Enregistré le: 16 Oct 2008, 15:24
-
 par Alicouu » 16 Oct 2008, 15:32
par Alicouu » 16 Oct 2008, 15:32
Bonjour,
J'ai besoin d'aide pour finir un exercice de maths, je suis bloquée aux dernières questions!
Voici l'énoncé :
On considère une suite (un) définie par son premier terme u0 et la relation de récurrence : pour tout entier naturel n, Un+1= (1/3) Un + 2.
1) Que peut-on dire de la suite (un) lorsque u0=3?
2) On supose désormais que u0 différent de 3.
Soit (vn) la suite définie sur N par : vn = Un + a, où a est un réel.
a) Déterminer le réel a de façon que la suite (vn) soit une suite géométrique de raison .
b) En déduire (vn) et (un) en fonction de n et U0.
c) En déduire que la suite (Un) est convergente et déterminer sa limite
3)a.Calculez la somme Sn = (soMmE ui) en fonction de n de premier terme i=0
b. Determiner sa limite de Sn/n quand n tend vers + infini.
J'ai fini jusqu'à la question 2)b. mais je ne sais pas comment montrer que (Un) est convergente et je n'arrive pas à calculer la somme.
Pouvez-vous m'aider svp ?
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Oct 2008, 16:16
par Imod » 16 Oct 2008, 16:16
Combien trouves-tu pour

et

à l'aide de

et

?
Imod
-
Alicouu
- Messages: 7
- Enregistré le: 16 Oct 2008, 15:24
-
 par Alicouu » 16 Oct 2008, 16:37
par Alicouu » 16 Oct 2008, 16:37
Alors je trouve :
Vn = (1/3)^n(u0-3)
Un = (1/3)^n(u0-3)+3
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Oct 2008, 16:50
par Imod » 16 Oct 2008, 16:50
Et que penses-tu de
^n)
quand n tend vers l'infini ?
Imod
-
Alicouu
- Messages: 7
- Enregistré le: 16 Oct 2008, 15:24
-
 par Alicouu » 16 Oct 2008, 16:54
par Alicouu » 16 Oct 2008, 16:54
lim (1/3)^n=0
Ce n'est pas la limite mon problème, c'est juste que je ne sais pas comment prouver qu'elle est convergente.
La seule propriété qu'on a vu pour les suites convergentes est qu'une suite croissant majorée est convergente ou qu'une suite décroissante minorée est convergente.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Oct 2008, 16:56
par Imod » 16 Oct 2008, 16:56
Dire qu'elle est convergente ou qu'elle a une limite c'est un peu la même chose ! Si tu prouves que la limite de

est 0 , tu prouves qu'elle est convergente du même coup .
Imod
-
Alicouu
- Messages: 7
- Enregistré le: 16 Oct 2008, 15:24
-
 par Alicouu » 16 Oct 2008, 17:01
par Alicouu » 16 Oct 2008, 17:01
La limite de Un est 3 non?
Ce qui m'embetait c'est que dans la formulation de la question on doit normalement prouver qu'elle est convergente avant de donner sa limite.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Oct 2008, 17:05
par Imod » 16 Oct 2008, 17:05
En effet la formulation peut gêner mais il est difficile de poser la question autrement .
Imod
PS : la limite est bien 3 :zen:
-
Alicouu
- Messages: 7
- Enregistré le: 16 Oct 2008, 15:24
-
 par Alicouu » 16 Oct 2008, 17:08
par Alicouu » 16 Oct 2008, 17:08
D'accord merc je montrerai donc que la limite est 3 pour finalement dire qu'elle est convergente.
Par contre je ne sais pas comment répondre à la question 3a.
Je sais que la somme d'une suite géo est Sn= 1er terme*(1-q^n+1)/(1-q)
Mais je bloque!
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Oct 2008, 17:14
par Imod » 16 Oct 2008, 17:14
Tu calcules la somme des

sachant que

est géométrique puis tu ajoutes un certain nombre de 3 pour obtenir la somme des

.
Imod
-
Alicouu
- Messages: 7
- Enregistré le: 16 Oct 2008, 15:24
-
 par Alicouu » 16 Oct 2008, 17:27
par Alicouu » 16 Oct 2008, 17:27
On ne connait ni u0 ni v0
En fait, cett suite est arithmetico géométrique et j'ai vu une formule pour la somme des ces suites qui donne ça (dans mon cas) :
Sn=(u0-3) * ((1-(1/3^n)^n+1)/(1-(1/3^n))+3(n+1)
Mais ça aboutit dans des calculs trop compliqués je ne sais pas comment faire pour simplifier l'écriture
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Oct 2008, 17:33
par Imod » 16 Oct 2008, 17:33
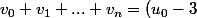(1+3^{-1}+3^{-2}+...+3^{-n}))
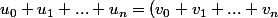+(3+3+...+3))
Je te laisse régler les détails !
Imod
-
Alicouu
- Messages: 7
- Enregistré le: 16 Oct 2008, 15:24
-
 par Alicouu » 16 Oct 2008, 18:57
par Alicouu » 16 Oct 2008, 18:57
Merci beaucoup je pense que c'est bon maintenant :)
Bonne soirée!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
