BONJOUR
je suis comme vous devez vous en douter en terminale , et il se trouve que comme tout bon terminale , j'éprouve quelques difficultées pour un des nombreux éxercices que nous donne régulièrrement notre prof de spé.
pour vous résumer , j'ai vraisment du mal ......
pouriez vous si il vous plait m'aider ?
Je vous remercie d'avance .
l'EXERCICE EN QUESTION :::::
Un entier naturel N dont le nombre de dizaines est noté D et dont le chiffre des unité est noté u , s'écrit :
N=10D+u
on considère N'=D+2u
1) Montrer que les solutions de l'équation 10x(congru)0(19) sont les entiers x tels que x(congru) 0(19) .
2) Démontrer que N est divisible par 19 si, et seulementsi, N' est divisible pas 19 .
3) En utilisant plusieurs fois de suite cette équivalence , étudier si le nombre 29431 est divisible par 19.
4)Dans cette question, on ne considère que des naturel N non divisible pas 19
-les nombres N et N' peuvent-ils être congrus modulo 19 ??
-on note r et r' les restes réspectifs des divisions de N et N' par 19 ; déterminer une realtion .
Congruence forever
6 messages
- Page 1 sur 1
Bonsoir
1.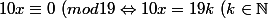)
19 divise 10 x et 19 est premier avec 10 donc d'après le théorème de Gauss, 10 divise x soit)
2. 10 D +U divisible par 19 équivaut à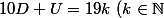) soit
soit 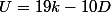
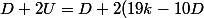=38 k -19 D=19(2k-D)) donc D+2U est divisible par 19.
donc D+2U est divisible par 19.
Même type de démonstration pour la réciproque.
3. D=2943 , U=1 , D+2U=2945
D=294 , U=5 , D+2U= 304
D=30 , U=4 , D+2U=38 ce nombre est divisible par 19 donc en remontant, 29431 est divisible par 19.
1.
19 divise 10 x et 19 est premier avec 10 donc d'après le théorème de Gauss, 10 divise x soit
2. 10 D +U divisible par 19 équivaut à
Même type de démonstration pour la réciproque.
3. D=2943 , U=1 , D+2U=2945
D=294 , U=5 , D+2U= 304
D=30 , U=4 , D+2U=38 ce nombre est divisible par 19 donc en remontant, 29431 est divisible par 19.
OUAA
Merçi beaucoup, C'est un peut d'éprinmant , ça à l'air si facile pour toi .
Au fait , vous pourriez peut étre m'aider, j'ai un problème spécifique à la spé math , c'est que je n'arrive pas du tout à faire les exos ,je ne sais pas si c'est parceque je suis incapable de les faires, si je ne travaille pas .... Mais l'orsque le prof corrige , La correction me paraît toute bête :hein:
Donc ça comence a m'enerver un peut , enfin , si c'est une situation qui vous est déja arrive dîte moi comment vous vous en êtes sortis ( ne me dît pas si vous ne vous en êtes pas sortis ) .
Enfin bon voilà , c'était mais problème existanciel ..
En tout cas merçi .
PS : j'ais aussi un peut de mal à savoir par ou partir quand je vois l'énnocer
Merçi beaucoup, C'est un peut d'éprinmant , ça à l'air si facile pour toi .
Au fait , vous pourriez peut étre m'aider, j'ai un problème spécifique à la spé math , c'est que je n'arrive pas du tout à faire les exos ,je ne sais pas si c'est parceque je suis incapable de les faires, si je ne travaille pas .... Mais l'orsque le prof corrige , La correction me paraît toute bête :hein:
Donc ça comence a m'enerver un peut , enfin , si c'est une situation qui vous est déja arrive dîte moi comment vous vous en êtes sortis ( ne me dît pas si vous ne vous en êtes pas sortis ) .
Enfin bon voilà , c'était mais problème existanciel ..
En tout cas merçi .
PS : j'ais aussi un peut de mal à savoir par ou partir quand je vois l'énnocer
Oui, je suis passé par cette situation. Et c'est plutôt fréquent comme problème.
Tu dis qu'en classe au moment de la correction, tu trouves les exercices 'bêtes'. Cela montre que tu comprends bien les solutions.
Pour t'en sortir voilà ce que je te conseille de faire :
1-Relis tes cours une fois de retour à la maison. Il est aussi très recommandé de faire de petites fiches pratiques qui résument l'ensemble des définitions, des propriétés et des théorèmes. Ceci t'aidera énormément à te rappeler ton cours.
2-Sache qu'il existe différents niveaux d'exercices.
Commence d'abord par des exercices de compréhension! Ces derniers impliquent une application directe du cours. Ensuite passe aux exerices un peu plus difficles. En plus du cours fraîchement étudié, ces exercices demandent généralement des prérequis.
Dans ce contexte il y a ensemble de techniques que tu dois développer : une sorte de boîte à outils.
3-Revois les exercices que vous corrigez en classe et essaies d'en sortir ces techniques.
4-Il existe une troisième catégorie d'exercices : ils sont les plus difficiles, généralement marqués d'une (*). Ces derniers demandent beaucoup plus d'imagination.
Mais pour résumer, je peux t'affirmer qu'au moins tu peux arriver aux exercices de niveau 2. Et c'est le cas de la majorité du commun des mortels, à mon avis:) Moyannant des efforts bien entendu!
Tu dis qu'en classe au moment de la correction, tu trouves les exercices 'bêtes'. Cela montre que tu comprends bien les solutions.
Pour t'en sortir voilà ce que je te conseille de faire :
1-Relis tes cours une fois de retour à la maison. Il est aussi très recommandé de faire de petites fiches pratiques qui résument l'ensemble des définitions, des propriétés et des théorèmes. Ceci t'aidera énormément à te rappeler ton cours.
2-Sache qu'il existe différents niveaux d'exercices.
Commence d'abord par des exercices de compréhension! Ces derniers impliquent une application directe du cours. Ensuite passe aux exerices un peu plus difficles. En plus du cours fraîchement étudié, ces exercices demandent généralement des prérequis.
Dans ce contexte il y a ensemble de techniques que tu dois développer : une sorte de boîte à outils.
3-Revois les exercices que vous corrigez en classe et essaies d'en sortir ces techniques.
4-Il existe une troisième catégorie d'exercices : ils sont les plus difficiles, généralement marqués d'une (*). Ces derniers demandent beaucoup plus d'imagination.
Mais pour résumer, je peux t'affirmer qu'au moins tu peux arriver aux exercices de niveau 2. Et c'est le cas de la majorité du commun des mortels, à mon avis:) Moyannant des efforts bien entendu!
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
