Calcul de somme

[Blacky]

Bonjour ! je suis actuellement en ECS2 (prépa HEC), et je lutte totalement sur un calcul de somme tout simple, et ça m'éneeerve ^^

Le voici :

On a n un naturel supérieur ou égal à 1.

Nous devons prouver que :

(Somme pour k=1 à n) 1/(2k+1) = (Somme pour k=1 à n)1/k - (1/2)(Somme pour k=1 à n)1/k +1

De une, désolé pour la lisibilité mais je n'ai pas encore trouvé comment mettre des symboles mathématiques (j'ai pas beaucoup cherché je l'avoue mais le temps me manque), de deux, j'aimerais bien une petite piste, un indice, car j'ai cherché un tas de changement d'indices à faire sans jamais trouver quelque chose de satisfaisant ><

Merci

[Clembou]

Bonjour ! je suis actuellement en ECS2 (prépa HEC), et je lutte totalement sur un calcul de somme tout simple, et ça m'éneeerve ^^

Le voici :

On a n un naturel supérieur ou égal à 1.

Nous devons prouver que :

(Somme pour k=1 à n) 1/(2k+1) = (Somme pour k=1 à n)1/k - (1/2)(Somme pour k=1 à n)1/k +1

De une, désolé pour la lisibilité mais je n'ai pas encore trouvé comment mettre des symboles mathématiques (j'ai pas beaucoup cherché je l'avoue mais le temps me manque), de deux, j'aimerais bien une petite piste, un indice, car j'ai cherché un tas de changement d'indices à faire sans jamais trouver quelque chose de satisfaisant ><

Merci

Note LaTeX :

• Somme : \sum_{k=0}^n
• Fraction : \frac{x}{y}

Ce qui donne :



Si je me suis trompé sur la traduction de l'énoncé, tu me le dis :++:

[fatal_error]

Salut,

la formule donnée au dessus doit pas etre bonne.
D'après Mapple :


edit : au passage quand on rentre le 1 en addition dans la somme ca fait pas le compte non plus. (Je dis ça je dis rien :happy2: )

[Joker62]

Ben euh oui là apparemment tu t'es trompé Clément :D

[Clembou]

Ben euh oui là apparemment tu t'es trompé Clément

Bah :triste: J'ai juste traduit en LaTeX ce que notre ami nous a marqué. :++: Apparement, il ne m'a toujours pas dit si c'était la bonne formule ou pas :p

[Joker62]

Ben j'sais pas si tu réfléchissais deux secondes sur ce que t'as écrit ? :)

[Clembou]

Ben j'sais pas si tu réfléchissais deux secondes sur ce que t'as écrit ?

Non mais pour moi, c'était clair sauf le +1 :++:

[Joker62]

Bé si c'est clair pourquoi t'as toujours un doute sur la validité de ta formule ?

Juste comme ça : A - (1/2)A + 1 = (1/2)A + 1

Après si tu crois toujours en ta formule tu fais ce que tu veux lol :D

[fatal_error]

On a l'impression que le but de l'exo c'est de faire apparaitre les nombres impairs et pairs, notamment en voyant les deux séries au lieu d'avoir tout groupé. Apres ya ptet des erreurs sur les recopiages d'indices, et bien sur, le +1 qui fait son rebel :zen:

Je propose cette formule :

[Clembou]

Bé si c'est clair pourquoi t'as toujours un doute sur la validité de ta formule ?

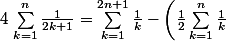Juste comme ça : A - (1/2)A + 1 = (1/2)A + 1

Après si tu crois toujours en ta formule tu fais ce que tu veux lol

Désolé ! :triste: Mais c'est pas moi qui a posté l'exercice lol

[Joker62]

C'est une discution interminable avec toi.
Ciao

[L.A.]

Bonsoir, j'essaye de passer entre les jets de casseroles pour aider ce pauvre Blacky.

la formule proposée au début est sans doute fausse : dans la deuxième somme, n à remplacer par (2n+1) ; et à la fin -1 au lieu de +1.
(sauf erreur)

Edit : la bonne est celle proposée par fatal_error

pour la montrer, je propose de partir de la somme de 1 à 2n+1 des 1/k, et de séparer les termes pairs et impairs ; truc classique pour évaluer la série
S1/(2k+1)² à partir de dzeta(2) = S1/k² = pi²/6.