Bonsoir à tous, je suis en TS et je n'arrive pas à résoudre ce problème, est-ce quelqu'un pourrait m'aider?
Soit f la fonction qui, à tout nombre complexe z différent de -2i associe:
Z=f(z)=(z-2+i)/(z+2i)
On appelle A et B les points d'affixes respectives:
zA=2-i et zB=-2i
En remarquant que Z=(z-zA)/(z-zB), déterminer:
1) L'ensemble E des points M d'affixe z, tels que Z soit un réel.
2) L'ensemble F des points M d'affixe z, tels que Z soit un imaginaire pur.
3) Calculer /f(z)-1/*/z+2i/, et en déduire que les points M' d'affixe Z, lorsque le point M d'affixe z parcourt le cercle de centre B et de rayon racine de 5, sont tous sur un même cercle dont on précisera le rayon et l'affixe du centre.
Merci beaucoup d'avance pour votre aide.
Nombres complexes
8 messages
- Page 1 sur 1
Salut ,je te donne qq indications:
on peut poser z=x+iy et on remplace ds f(z), tu obtiendras une certaine expression où il faudra que tu separes bien la partie reelle de la partie imaginaire
1)pour que Z soit reel il faut que Im(Z)=0.tu as trouvé ta partie imaginaire au dessus donc tu resous l'equation trouvé ce qui te donneras l'ensemble des pts demandés
2)pour que Z soit imaginaire pur il faut que Re(Z)=0.tu as trouvé ta partie reelle au dessus donc tu resous l'equation trouvé ce qui te donneras l'ensemble des pts demandés
3) le debut de la question est calculatoire ce n'est pas bien difficile et sers toi des questions precedentes.
A+
on peut poser z=x+iy et on remplace ds f(z), tu obtiendras une certaine expression où il faudra que tu separes bien la partie reelle de la partie imaginaire
1)pour que Z soit reel il faut que Im(Z)=0.tu as trouvé ta partie imaginaire au dessus donc tu resous l'equation trouvé ce qui te donneras l'ensemble des pts demandés
2)pour que Z soit imaginaire pur il faut que Re(Z)=0.tu as trouvé ta partie reelle au dessus donc tu resous l'equation trouvé ce qui te donneras l'ensemble des pts demandés
3) le debut de la question est calculatoire ce n'est pas bien difficile et sers toi des questions precedentes.
A+
Bonjour
Dans ton cours, tu as du voir que=(\vec {BM},\vec {AM}))
Un réel a pour argument) donc on doit avoir
donc on doit avoir =0+k\pi) ce qui équivaut à dire que les vecteurs
ce qui équivaut à dire que les vecteurs  et
et 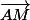 sont colinéaires donc l'ensemble des poits M est la droite (AB) privée du point B.
sont colinéaires donc l'ensemble des poits M est la droite (AB) privée du point B.
Pour la deuxième question , un imaginaire pur a pour argument donc tu peux en déduire une propriété des vecteurs.
donc tu peux en déduire une propriété des vecteurs.
Dans ton cours, tu as du voir que
Un réel a pour argument
Pour la deuxième question , un imaginaire pur a pour argument
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
