Olympiade Australienne

[Zweig]

Soit ABC un triangle et soit la bissectrice interne de l'angle A rencontrant le cercle circonscrit au point P. On définit les points Q et R d'une manière similaire.

Montrer que

[CENTER][/CENTER]

[Mhdi]

D'aprèsl'inégalité triangulaire :



En sommant on obtient (*)
R, A, Q, C, P, et B appartiennent au cercle dont le centre est I. Donc,

On remplace dans (*) :
On sait que :



=>

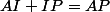
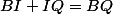
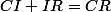
[Imod]

Attention , est le centre du cercle inscrit dans .

Imod

[Mhdi]

Je me disais aussi que c'était trop facile...

[ThSQ]

Très joli problème.


( En regardant les angles (bissectrice) on a R = PI = PB = PC, après on applique l'inég triangulaire (BC < BI+IC par ex) et on somme )

[Imod]

Ces problèmes d'angles sont toujours très jolis car souvent bien cachés !!!

Imod

[khalilou]

Soit ABC un triangle et soit la bissectrice interne de l'angle A rencontrant le cercle circonscrit au point P. On définit les points Q et R d'une manière similaire.

Montrer que

[CENTER][/CENTER]

slt tt le monde ;ma réponse est :
BQ+QC >=BC ET RC+RB >=BC
RC+AR >=AC ET AP+PC >=AC
BQ+AQ >=AB ET AP+BP >=AB
on fai une addition coté par coté et on obtient :
2(AP+BQ+CR)+RB+AR+AQ+QC+PC+PB >=2(AB+BC+AC)
et donc on deduit ke :
AP + BQ + CR > AB + BC + AC