Formule combinatoire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lezard
- Messages: 3
- Enregistré le: 15 Mai 2008, 21:34
-
 par lezard » 15 Mai 2008, 21:41
par lezard » 15 Mai 2008, 21:41
Bonjour,
Je cherche à calculer la somme pour k variant de 0 à N de N*CN(en indice)k(en exposant)
Je me demande si il y a une formule qui permette de faire le calcul rapidement.
Je vous remercie pour votre aide.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 15 Mai 2008, 21:52
par Joker62 » 15 Mai 2008, 21:52
Hum :)
Développe donc (1+x)^n
Hummmm
Dérive donc (1+x)^n
Hummmmmmmm
Conclusion :D
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 15 Mai 2008, 22:01
par Quidam » 15 Mai 2008, 22:01
lezard a écrit:Bonjour,
Je cherche à calculer la somme pour k variant de 0 à N de N*CN(en indice)k(en exposant)
Je me demande si il y a une formule qui permette de faire le calcul rapidement.
Je vous remercie pour votre aide.
Oui, il y en a une ! Mais je ne la connais pas par coeur !
Pour la retrouver, tu peux dire que :
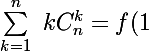)
avec
=\sum_{k=1}^n \ kx^{k-1}C_n^k)
Une primitive de f est alors F :
=\sum_{k=0}^n \ C_n^k\ x^k)
qui n'est autre que
^n)
je te laisse terminer...
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 15 Mai 2008, 22:02
par Quidam » 15 Mai 2008, 22:02
Joker62 a écrit:Hum

Développe donc (1+x)^n
Hummmm
Dérive donc (1+x)^n
Hummmmmmmm
Conclusion

Désolé Joker ! Je n'avais pas vu ta réponse !
-
lezard
- Messages: 3
- Enregistré le: 15 Mai 2008, 21:34
-
 par lezard » 15 Mai 2008, 22:09
par lezard » 15 Mai 2008, 22:09
En fait, je me suis trompé. Ce que je cherche à calculer, c'est :
la somme pour k variant de 0 à N de k*CN(en indice)k(en exposant)
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 15 Mai 2008, 22:28
par Quidam » 15 Mai 2008, 22:28
lezard a écrit:En fait, je me suis trompé. Ce que je cherche à calculer, c'est :
la somme pour k variant de 0 à N de k*CN(en indice)k(en exposant)
oui, bien sûr, j'avais mal lu et j'avais répondu à cette dernière question, non sans faire moi aussi la confusion entre n et k. C'est corrigé, remonte voir ma réponse précédente.
-
lezard
- Messages: 3
- Enregistré le: 15 Mai 2008, 21:34
-
 par lezard » 15 Mai 2008, 22:36
par lezard » 15 Mai 2008, 22:36
Merci pour votre aide!
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 15 Mai 2008, 23:19
par Joker62 » 15 Mai 2008, 23:19
Pas de soucis :D
Il s'avère finalement que ça servait à rien.
M'enfin bon, j'retourne révisé frustré de ce fait ;)
Bonne soirée tout le monde

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 15 Mai 2008, 23:32
par raito123 » 15 Mai 2008, 23:32
Hey ¨dîtes moi que c'est faux :
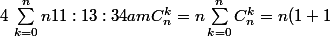^n = n2^n)
Hein ...?
Les multiples ne doivent pas être utilisés sans nécessité
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 16 Mai 2008, 06:30
par Quidam » 16 Mai 2008, 06:30
raito123 a écrit:Hey ¨dîtes moi que c'est faux :
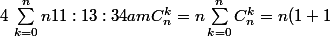^n = n2^n)
Hein ...?
Non, c'est correct !
Dans ma réponse, j'avais fait une erreur qui est maintenant corrigée ! La somme recherchée est en fait :

Désolé d'avoir semé la confusion...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
