Probabilité

[ice456]

Bonjour,

j'ai du mal à comprendre la différence entre "densité de probabilité" et "fonction de répartition".

Pourriez-vous m'indiquer à quoi elles servent exactement?

Pour moi une densité de probabilité c'est une fonction qui permet d'attribué une probabilité sur un interval [a,b] (donc dans le cas continue) et tel que .

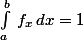
Et la fonction de répartition c'est la primite de la densité de probabilité f.

Est ce que la fonction de répartition n'est à utlisé que dans un cas précis?

Merci

[Kriegger]

F(x) = P(X <=x ) = int(-inf,x) f(t) dt

[ice456]

ok c'est pour la fonction de répartition ça je supose...
Et concrètement elle sert à quoi cette fonction?

En ce qui concèrne la densité de probabilité elle sert bien à munir un interval d'une loi de probabilité?

[Kriegger]

F(x) = P(X <=x )

elle sert à obtenir ca une probabilité ^^ tu n'as pas de probabilité à partir de la densité. La densité finalement ne donne qu'une fréquence des éléments de ta variable X.

[ice456]

Ok merci c'est plus clair maintenant

[ice456]

Pour être sur d'avoir bien compris....

Soit la loi de probabilité donnée par la fonctin de répartition suivante :

(x) = 0 pour x 0
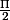
(x) = arcsin x pour 0 x 1
(x) = 1 pour x > 1

Calculer la densité de probabilité correspondante.

Pour celà je calcule donc la dérivée de la fonction de répartition puisque fonction de répartition = primitive de la denstié de proba (dans le cas continu)

J'obtiens donc pour la densité de probabilité :

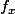
(x) = 0 pour x 0
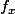
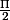
(x) = pour 0 x 1
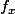
(x) = 0 pour x > 1

Mon raisonnement est-il correct?
Merci

[alavacommejetepousse]

oui
si ce n'est qu' une fonction ne peut pas prendre deux valeurs distinctes au même point donc [B]x1

[ice456]

ok merci de me l'avoir signalé