Factorisation

[sissokomad]

Bonjour
J'essai de factoriser
x4 - 6x² - 8x - 3
Sachant que la racine du polynome est -1
J'ai essayer par x - a mais je suis bloqué pendant la resolution puisque je tombe sur une expression de degré 3 dont je ne connait pas les racines.
Merci de votre aide

[guigui51250]

Bonjour
J'essai de factoriser
x4 - 6x² - 8x - 3
Sachant que la racine du polynome est -1
J'ai essayer par x - a mais je suis bloqué pendant la resolution puisque je tombe sur une expression de degré 3 dont je ne connait pas les racines.
Merci de votre aide

Salut

Mets tu polynome sous la forme (x+1)(ax^3+bx²+cx+d)
tu développes, tu fait un système entre les a, b, c et d du polynome de départ et le polynome que tu trouve en développant et tu retrouve a, b, c et d du polynome sous la forme (x+1)(ax^3+bx²+cx+d)

Byyeeee

[sissokomad]

oui c'est ce que j'ai fait et je tombe sur :

(x + 1)(x^3 - x² - 5x -3 )
et je n'arrive pas a factoriser le second terme

[nuage]

Salut,
Ce que tu as fais est juste (ou alors j'ai fait la même erreur).
Essaye de regarder la valeur de pour .

[saintlouis]

Bonjour

Bonne idée " nuage"

[sissokomad]

oui c'est vrai que - 1 est aussi racine du second terme .Mais quel raisonnement me permettrait de trouvé cela .En fait cet exo est tiré d'un cour ou on donne la solution mais sans le raisonnement.

[XENSECP]

bon tu en es où ?

[sissokomad]

En fait j'en suis toujour a l'etape :

(x + 1)(x^3 - x² - 5x -3 )
je n'arrive pas a factoriser le second terme .Quel est le raisonnement a suivre pour connaitre les racine du second termes ?
C vrai que Mr nuage a raison -1 est l'une des racine du second terme Mais par quel raisonnement peut on le trouvé?

[XENSECP]

ba tu refais la même chose, sahcant que -1 est encore racine !

[sissokomad]

Mais par quel formule sait on que -1 est racine du second terme.
Ou bien c'est un choix après essai ?

[MABYA]

Quand on a une équation faut toujours regarder si une racine n'est pas apparente en faisant f(1),f(-1)
f(2),f(-2) jusqu'à 5 et plus
Il n'y a pas de formule,
C'est surtout les coefficients qui sont proches ou multiples qui attirent l'attention.
Pour l'autre racine on se sert de c/a= x'.x"" ou/et b/a= x'+x".

[Ben314]

Salut,
Je sais pas en quelle classe tu es, mais, si tu as fait un peu d'arithmétique, il y a un petit résultat sympa qui peut être utile dans des cas comme celui là :
Si est un polynôme dont tout les coefficients sont entiers et si 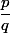est une racine du polynôme alors divise et divise .
C'est très facile à démontrer.

Par exemple, dans le cas du polynôme , ça te dit que, si éventuellement il y a une racine rationnelle, ça ne peut être que 1, 3, -1 ou -3.

Si tu as jamais fait d'arithmétique, tu laisse tomber ce résultat que tu verra plus tard.