Théorie de la mesure

[Francisfrancis]

Bonjour j'aurais besoin d'aide pour trouver une réponse à cet énoncé (autrement que par l'absurde):

Données:
{fn} et f définie sur (espace mesuré) à valeur dans R, E est l'ensemble des points x de X où {fn} converge vers f.
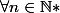
et on note:


Merci à vous bonne journée.

[Joker62]

Salut

ça s'apelle la convergence en mesure.
En TD, on l'a démontrer en 2 sous questions que je t'écris :

1) En remarquant que la fonction x/(1+x) est strictement croissante, montrer que (f_n) converge en mesure vers f si et seulement si

2) En déduire que si (f_n) converge presque partout vers f, alors (f_n) converge en mesure vers f

Je rapelle la définition de la convergence en mesure :
On dit que f_n converge en mesure vers f si

[Francisfrancis]

Je te remercie mais en fait je n'ai pas encore vu la convergence de mesure donc je ne peux pas l'utiliser, désolé je n'ai pas précisé.