Soit
On désignera par
Pour tout
Montrer que
On pose :
Questions :
J'ai resolu
Merci d'avance !!
Theorie de la mesure !
38 messages
- Page 1 sur 2 - 1, 2
Theorie de la mesure !
par barbu23 » 13 Nov 2007, 14:35
Bonjour :
Soit $)
un espace mesuré.
On désignera par
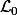
( resp. 
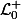
) l'ensemble des applications mesurables de  $)
da,s  $)
( resp . dans  $)
).
Pour tout
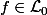
et tout 
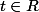
, on posera :
 = \mu( \{ \omega \in \Omega : f(x) > t \} ) $)
.
 $)
Soit .
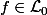
Montrer que
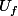
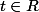
est décroissante et que pour tout , on a :
 = U_{f}(t) $)
.
 $)
Soit _{n \geq 0} $)
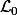
une suite croissante dans qui converge simplement vers 
, montrer que la suite  _{n \geq 0} $)
est croissante et converge simplement vers .
 $)
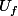
Soient 
, 
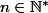
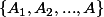
une partition de 
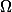
constituée d'éléments de 
et 
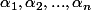
des rééls vérifiant 
.
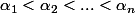
On pose :
.
 $)
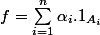
Calculer, suivant les valeurs de 
,  $)
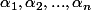
en fonction de et de  , ... \mu (A_{n}) $)
.
Questions :
J'ai resolu et , il me reste le ... Est ce que vous pouvez m'aider sur cette dernière question ?
Merci d'avance !!
Soit
On désignera par
Pour tout
Montrer que
On pose :
Questions :
J'ai resolu
Merci d'avance !!
par legeniedesalpages » 13 Nov 2007, 15:04
salut,
tu sépares les
qui sont 
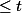
et les qui sont 
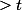
, non?
si il existe j tel que pour tout
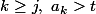
, >t \})
, et même ces 
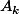
forment une partition de >t \})
. On utilise alors la sigma-additivité.
tu sépares les
si il existe j tel que pour tout
par barbu23 » 13 Nov 2007, 15:47
Oui , alors, supposons que :
: 
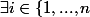
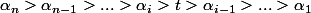
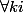
: = \displaystyle \sum_{ i=0}^{n} \alpha_{i} . \mathbb{1}_{A_{i}}(x) = \alpha_{k} \} \subset \{ x \in \Omega \hspace{10cm} : \hspace{10cm} f(x) = \displaystyle \sum_{ i=0}^{n} \alpha_{i} . \mathbb{1}_{A_{i}}(x) > t \} = \{ x \in \Omega \hspace{10cm} : \hspace{10cm} f(x) = \displaystyle \sum_{ i=0}^{n} \alpha_{i} . \mathbb{1}_{A_{i}}(x) \in \{ \alpha_{i} t \} $)
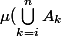 = \displaystyle \bigcup_{k=i}^{n}\{ x \in \Omega \hspace{10cm} : \hspace{10cm} f(x) = \displaystyle \sum_{ i=0}^{n} \alpha_{i} . \mathbb{1}_{A_{i}}(x) = \alpha_{k} \} = \mu ( \{ x \in \Omega \hspace{10cm} : \hspace{10cm} f(x) = \displaystyle \sum_{ i=0}^{n} \alpha_{i} . \mathbb{1}_{A_{i}}(x) > t \} ) $)
 = \displaystyle \sum_{k \geq i} \mu (A_{k} ) $)
Il y'a une erreur parceque il faut soit écrit aussi en fonction des 
..
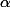
Est ce que vous pouvez m'aider là ?
Merci d'avance !!
Il y'a une erreur parceque il faut
Est ce que vous pouvez m'aider là ?
Merci d'avance !!
par legeniedesalpages » 13 Nov 2007, 16:12
Je ne pense pas qu'il y ait une erreur, l'entier i qui sert d'indexation de ta somme dépendant des )
par barbu23 » 13 Nov 2007, 18:51
Il reste encore une petite question :
Comparer d.\lambda $)
et  d\mu $)
où 
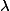
est la mesure de Lebesgue sur  $)
.
Merci d'avance !!
Comparer
Merci d'avance !!
par legeniedesalpages » 13 Nov 2007, 22:35
pour celle que tu as trouvé je suis d'accord, mais pour l'autre je ne vois pas du tout. :triste:
par barbu23 » 13 Nov 2007, 23:09
D'après :
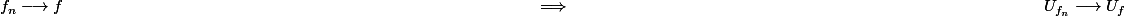
D'après "Beppo - Levi" :
 d \lambda= \displaystyle \lim_{ n \longrightarrow + \infty} \int_{\mathbb{R}_{+}} U_{f_{n}}(t) d \lambda $)
ça peut aider ça "legeniedesalpages" ?
D'après "Beppo - Levi" :
ça peut aider ça "legeniedesalpages" ?
par legeniedesalpages » 13 Nov 2007, 23:14
le beppo levi que je connais ne marche que pour les suites croissantes, et dans 2) tu parles de suites décroissantes non?
par barbu23 » 13 Nov 2007, 23:42
Ah non !! :lol2: là c'est la 
ème question que je resout !mais on a pas terminer la 
ème question :
La ème question dit :
 $)
Montrer que pour 
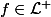
, on a :  d \lambda = \int f(x) d \mu $)
.
Donc, il faut d'abord, resoudre la ème question, il y'a égalité aussi je pense!! non ?
La
Donc, il faut d'abord, resoudre la
par Imod » 13 Nov 2007, 23:46
Je parle sans doute pour moi , si ce sujet se poursuivait en messages personnels , je n'y verrais pas d'offence !!!
Imod
Imod
par legeniedesalpages » 14 Nov 2007, 00:15
alors on est à quelle question en fait, barbu là j'ai du mal à suivre, :dodo:
imod, non plus c'est pas très clair ce que tu dis :marteau:
imod, non plus c'est pas très clair ce que tu dis :marteau:
38 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :