Topologie quotient

par **entrecieletmer16** » 30 Déc 2007, 10:13

Bonjour,

J'aimerais démontrer ce théorème mais je ne sais pas très bien comment m'y prendre. J'ai déjà montré (2) implique (3).

Théorème:

Soit X un espace de Hausdorff compact et soit ~ une relation dequivalence sur X.
Notons GAMMA = {(x,y) appartient à X × X : x ~ y} le graphe de la relation ~. Montrer que les énoncés suivants sont équivalents :

(1) La projection canonique PI : X --> X/~ est fermée cest-à-dire envoie les fermés sur des fermés.

(2) Le quotient X/~ est Hausdorff.

(3) Le graphe GAMMA est fermé dans X × X.

Pourriez-vous m'aider à démontrer les autres implications ?
Merci de votre aide

par **ThSQ** » 30 Déc 2007, 15:29

De la topo :++: :langue:

Un essai pour : 1 => 2

Soit pi(x) et pi(y) deux points distincts de X/~

Quelques aller-retour entre X et X/~ :

* x et y sont fermés dans X qui est Haussdorff (= séparé in french in ze text ?), pi est fermée donc pi(x) et pi(y) sont fermés dans X/~.
* pi est C° donc

est fermé, pareil pour K2.
* K1 et K2 sont des compacts disjoints dans un compact, on peut les "séparer" par des ouverts U1 et U2 (ie Ui disjoints et Ui contient Ki) : on recouvre U1 par des ouverts disjoints de U2 (possible car X séparé) et on prend un sous-recouvrement fini (possible car compact) dont l'union est un ouvert disjoint de U2 qui contient K1. On recommence avec K2 qui contient un recouvrement disjoint de U1, .....
* F1 = p(X \ U1) est fermé, O1 = X/~ \ F1 est un ouvert (trophor). Pareil pour U2. O1 et O2 sont deux ouverts,

et

, et ils sont disjoints (faire un dessin !).

Donc X/~ est séparé !

par **ThSQ** » 30 Déc 2007, 17:59

3 => 1

Soit donc A un fermé (et donc compact) de X. On veut montrer que p(A) est fermé. p(A) fermé ssi

est fermé par déf. de la topologie quotient.

(ie le "saturé" par ~).

B est un "tranche" de GAMMA.

Les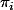

sont continues (pratiquement par déf de la topo produit cette fois) et on a :

Allons-y calmement :

est un fermé

est donc aussi un fermé et donc un compact.

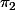étant C° l'image d'un compact est un compact et donc un ... fermé ! :zen:

par **entrecieletmer16** » 13 Jan 2008, 12:28

Bonjour,

Sans vouloir abuser de votre temps et de vos connaissances, je me permets de vous poser encore une question. Comment démontrer qu'un singleton est fermé dans un espace de Hausdorff ? J'ai l'idée en tête, mais je ne vois pas comment l'écrire.

Merci pour votre collaboration.

Bien à vous

par **tize** » 13 Jan 2008, 12:45

Bonjour,
si ton espace E est séparé alors

est fermé car pour tout

,

il existe deux ouverts

et

tels que

,

et

. Tu peux alors remarquer que

est un ouvert, donc...

par **ThSQ** » 13 Jan 2008, 13:05

Il suffit même de remarquer qu'il existe un ouvert U contenant y et ne contenant pas x (c'est moins fort que séparé, "T1" je crois).

par **tize** » 13 Jan 2008, 14:06

"T1" ?! Connais pas du tout...je vais me renseigner, merci :we:
Mais tu m'as l'air complètement accroc à la Topo ThSQ :++:

par **ThSQ** » 13 Jan 2008, 14:30

http://fr.wikipedia.org/wiki/Espace_T1

La topo c'est ce que je préfère, cette étude de la notion, toute relative, de proximité est fascinante. :we:

par **tize** » 13 Jan 2008, 14:36

Merci pour le lien... :we:

Topologie quotient

Topologie quotient

Qui est en ligne