Espace vectoriel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 05 Jan 2008, 19:40
par Ewok » 05 Jan 2008, 19:40
Bonsoir,
Je suis bloquée sur un exo sur les espaces vectoriels depuis un certain temps...bref un ptit coup de main serait le bienvenu! Voici le sujet:
Soit

défini par:
(X)=P(X+1)-P(X))
.
On définit
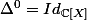
et
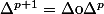
.
Montrer que si P est un polynôme de degré n,
\neq0)
et
=0)
. Prouver alors que:
=P(0)+\frac{\{X\}}{1{!}}\Delta P(0)+...+\frac{\{X\}^k}{k{!}}\Delta^k P(0)+...+\frac{\{X\}^n}{n{!}}\Delta^n P(0))
avec pour tout
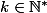
,
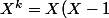...(X-k+1))
.
Voilà le seul truc que j'ai réussi à faire, c'est à montrer que
=0)
...c'est pas glorieux je sais^^
Merci d'avance pour votre aide!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Jan 2008, 20:19
par yos » 05 Jan 2008, 20:19
Bonsoir.
Montre l'égalité pour X=0,1,...,n
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 05 Jan 2008, 20:47
par Ewok » 05 Jan 2008, 20:47
Euh j'ai pas très bien compris ce que tu proposes...récurrence forte? mais X n'est pas nécessairement un entier, si?...
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 05 Jan 2008, 20:54
par emdro » 05 Jan 2008, 20:54
Bonsoir,
si deux polynômes de degré n coïncident pour n+1 valeurs, alors...
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 05 Jan 2008, 21:02
par Ewok » 05 Jan 2008, 21:02
Ah (au pif) ils sont égaux? si c'est le cas je savais pas...
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 05 Jan 2008, 21:04
par emdro » 05 Jan 2008, 21:04
Eh oui, ils sont égaux.
Et c'est ce qui te permettra d'utiliser la remarque de Yos.
Bon courage...
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 05 Jan 2008, 21:06
par Ewok » 05 Jan 2008, 21:06
Ah va falloir que je démontre ça en plus...bon j'vais essayer merci à tous les deux!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Jan 2008, 21:11
par yos » 05 Jan 2008, 21:11
Ewok a écrit:Ah va falloir que je démontre ça en plus
C'est immédiat car P-Q peut pas avoir plus de n racines sauf s'il est nul.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 05 Jan 2008, 21:13
par Joker62 » 05 Jan 2008, 21:13
Pour démontrer le résultat sur les polynômes pense aux racines de P-Q
où P et Q sont les polynômes en question qui coïncide aux n+1 points.
Ahhh la grippe m'a volé 2 minutes !
J'vais aller m'coucher lol
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 05 Jan 2008, 21:19
par Ewok » 05 Jan 2008, 21:19
En fait le problème c'est qu'on n'a absolument pas traité de polynômes en cours pour l'instant donc s'il faut que je démontre aussi le résultat sur les racines...on n'est pas sorti de l'auberge (même si je peux recopier la démo du deschamps c'est vrai) :lol2:
-
SimonB
 par SimonB » 06 Jan 2008, 03:07
par SimonB » 06 Jan 2008, 03:07
Question théoriquement pas jolie mais utilement utile (quoique il semble y avoir une redondance) : à quel niveau étudies-tu ?
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 06 Jan 2008, 11:08
par Ewok » 06 Jan 2008, 11:08
En MPSI (mea culpa j'voulais le mettre dans le titre du sujet mais...j'ai zappé)
-
SimonB
 par SimonB » 06 Jan 2008, 13:27
par SimonB » 06 Jan 2008, 13:27
Et pas de cours sur les polynômes, tu es sûre ? Dans ce cas-là, je vois vraiment pas quoi faire :-(
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 06 Jan 2008, 13:56
par Ewok » 06 Jan 2008, 13:56
C'est un DM exclusivement sur les espaces vectoriels... :triste:
-
SimonB
 par SimonB » 06 Jan 2008, 13:58
par SimonB » 06 Jan 2008, 13:58
Ce n'est pas la question que je pose ; y a-t-il déjà eu un chapitre dans le cours de l'année où vous avez parlé de polynômes ? (Normalement, oui)
En maths, il est courant d'utiliser des choses anciennes...
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 06 Jan 2008, 14:27
par Ewok » 06 Jan 2008, 14:27
Non non, jamais eu de cours sur les polynômes cette année (d'ailleurs apparemment on n'a pas abordé le programme dans l'ordre habituel)...
-
Ewok
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Sep 2007, 21:19
-
 par Ewok » 06 Jan 2008, 21:56
par Ewok » 06 Jan 2008, 21:56
Jme permets de remonter mon sujet qui est en train de sombrer alors que j'ai toujours pas trouvé :p
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
