Probléme de suite

[basket]

Bonjour

soit la suite définie par
Un+2 = racine de Un+1 + Un

déduire qu'il existe No tel que N >= No on est Un >= racine de 2

[ThSQ]

Manque à l'évidence les conditions initiales : si u0=u1=0 la suite est nulle.

[basket]

j'ai oublié de le dire

u0>0 et u1> 0

[Purrace]

Fais une recurrence.

[basket]

j'ai déjà essayé mais je n'arrive à rien

[Purrace]

En fait c'est racine(Un+1 + Un) ou racine(Un+1)+rac(Un) , on comprend pas bien.

[basket]

c'est Un+2 = racine de (Un+1 + Un)

[Purrace]

Ta juste a remarquer que ta suite est croissante ( je pense l'est pas etudier ) alors si vn>ou=2 vn+1 aussi d'ou la reccurence. Si c'est pas le cas alors dit le moi.

[basket]

oui mais on parle pas de No et Un>= à racine de 2

[Purrace]

Ta reussit a etudier les variations de ta suite.

[basket]

oui j'ai montrer qu'elle était croissante

[alben]

oui j'ai montrer qu'elle était croissante

Bravo !
Le problème c'est qu'elle n'est pas croissante sauf si (u0+u1)<2 :we:

[yos]

elle n'est pas croissante sauf si (u0+u1)<2

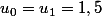
Avec elle croit aussi.

[basket]

elle est croissante ou décroissante :marteau:

[ThSQ]

Si u0 et u1 sont >= 1 c'est clair.

Si u0 ou u1 < 1.
0 < a = min(u0,u1) et n_0 = E(2/a)+1

Alors j'affirme que u(n_0) >= sqrt(2).

-u(2) >= sqrt(a+a) = sqrt(2) * sqrt(a)
-u(3) >= sqrt(sqrt(2*a) + a)
So 2*a < 1, sqrt(2*a) >= 2*a et donc u(3) >= sqrt(2*a + a) = sqrt(3*a)

Récurrence : si 1 >= u(k) >= sqrt(k*a) avec k < n_0 alors 1 >= u(k+1) >= sqrt((k+1)*a)
...
u(n_0) >= sqrt(n_0 * a) >= sqrt(2)

[basket]

:crash: bravo pour la démo mais j'ai du mal à suivre

[basket]

:help: :help: :help: