Théorie des ensembles
20 messages
- Page 1 sur 1
théorie des ensembles
j'ai du mal à démontrer les questions A et B
H1 ( A intersection B' intersection C' )
H2 ( A intesrsection B ) U C
A / H1 U H2
B / H1 intersection H2
j'ai utilisé la loi de morgane mais je me suis blocké
et merci
B' : ça veut dire B barre
H1 ( A intersection B' intersection C' )
H2 ( A intesrsection B ) U C
A / H1 U H2
B / H1 intersection H2
j'ai utilisé la loi de morgane mais je me suis blocké
et merci
B' : ça veut dire B barre
si 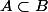 , alors
, alors 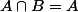 .
.
Comme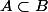 , si tu prends un élément x de A, c'est aussi un élément de B.
, si tu prends un élément x de A, c'est aussi un élément de B.
Donc x appartient à A et à B, c'est à dire x appartient à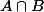 .
.
Réciproquement si x est dans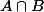 , x est par définition dans A.
, x est par définition dans A.
Par conséquent on a bien l'égalité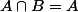 .
.
(Si tu as du mal revois la définition de l'intersection de deux ensembles dans ton cours).
Mais en fait pas besoin d'utiliser autant de fois cette propriété.
Pour les lignes je te fais les premières:
\cup [(A\cap B)\cup C]\\<br />=(A\cap \overline{B} \cap \overline{C})\cup [(A\cup C)\cap(B\cup C)]\\<br />=[(A\cap \overline{B} \cap \overline{C})\cup (A\cup C)]\cap [(A\cap \overline{B} \cap \overline{C})\cup (B\cup C)])
tu vois que\cup (A\cup C)] = A\cup C) car
car \subset (A\cup C)) ,
,
et tu montres que\cup (B\cup C)] = A\cup B\cup C) .
.
Comme tu as\subset (A\cup B \cup C)) , tu en déduis de la propriété que je t'ai dit que
, tu en déduis de la propriété que je t'ai dit que \cap (A\cup B \cup C) = A\cup C) .
.
(sauf erreur de ma part)
Comme
Donc x appartient à A et à B, c'est à dire x appartient à
Réciproquement si x est dans
Par conséquent on a bien l'égalité
(Si tu as du mal revois la définition de l'intersection de deux ensembles dans ton cours).
Mais en fait pas besoin d'utiliser autant de fois cette propriété.
Pour les lignes je te fais les premières:
tu vois que
et tu montres que
Comme tu as
(sauf erreur de ma part)
legeniedesalpages a écrit:si, alors
.
Comme, si tu prends un élément x de A, c'est aussi un élément de B.
Donc x appartient à A et à B, c'est à dire x appartient à.
Réciproquement si x est dans, x est par définition dans A.
Par conséquent on a bien l'égalité.
(Si tu as du mal revois la définition de l'intersection de deux ensembles dans ton cours).
Mais en fait pas besoin d'utiliser autant de fois cette propriété.
Pour les lignes je te fais les premières:
tu vois quecar
,
et tu montres que.
Comme tu as, tu en déduis de la propriété que je t'ai dit que
.
(sauf erreur de ma part)
j'ai pas compris pourtant le prof nous a donné un coup de pouce
il nous a dit de transformer H1 en A intersection ( B U C ) tout complément
ça veut dire : B union C tout barre
legeniedesalpages a écrit:oui c'est ce que j'ai aussi fait, d'abord j'ai modifié, et puis à la fin j'ai modifié
de la même façon que ton prof pour obtenir le résultat voulu.
Le mieux c'est que tu me dises précisément quel point tu n'as pas compris (genre quelle égalité tu bloques)
j'ai pas compris la ligne qui commence pas " tu vois que .... "
je m'excuse pour mon français
théorie des ensembles
legeniedesalpages a écrit:voilà (enfin pour cette ligne).
malheuresement c'est faux notre prof aujourd'hui nous a lancé un défi , il nous a dit que la solution de /A est égale à : A !!!
et nous a dit de bien démontrer cela !! :doh: :mur:
legeniedesalpages a écrit:Tu as donné cet énoncé
On voit clairement que H1 U H2 n'est pas forcément égal à A, par exemple tu prends:
A=[0,1],
B'=C'=B= ensemble vide,
C=[0,200]
H1 U H2= [0,200], qui n'est pas égal à A.
vous pouviez regarder là monsieur ??
http://www.mathsfaciles.com/fr/theoreme-ensemble-question-mathematiques-1068.php
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
