Denombrement

[cadi]

bonjour encore un peu d'aide si vous le voulez bien

Soit R={
et ={ pour k=0,..,n
a) montrer que est un partage de R
b) montrer que . en deduire #R
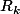
(là je pense qu'il faut sommer les de 0 à N et trouve R puisque l'on a un partage)
c)generaliser au cas de S={ dont on determinera le cardinal.

[fahr451]

bonjour

somme t on vraiment des parties ...?

[cadi]

non escuse moi on somme le cardinal des Rk

[fahr451]

y a un tit souci que représente N ?

N = {1,....,N } ?

[cadi]

N est un ensemble à n elements

[fahr451]

alors

soit (A,B) dans R, A a un certain cardinal (unique!) k dans {0,...n} ce qui assure que A est dans un et un seul Rk


ce qui assure que les Rk forment un partage

pour déterminer un élément (A,B) de Rk on détermine d'abord A il ya

k parmi n façons de choisir A (partie de N a k éléments )

et ensuite pour déterminer B qui doit vérifier AUB = N

on dit que B = A ' U B' où A ' est lecomplémentaire de A dansN et B' n'importe quelle partie de A'

donc il faut et il suffit de construire la partie B' il y a 2^k parties dans A

et le résultat

card R = sigma card Rk = 3^k