Maximisation de la trace

[Christophe Genolini]

Bonjour,

Je travaille actuellement sur des matrices carré NxN. Je cherche à trouver la (ou une) permutation de colonnes qui maximiserait la trace. Pour des tailles petites (genre N <=4), j'ai programmé un calcul exaustif de toutes les combinaisons possible et je teste toutes les traces. Mais pour N plus grand (genre N=10), ca devient impossible.

Connaissez-vous la solution à ce problème ?

Merci de votre aide...

Christophe

[Lierre Aeripz]

Pour une matrice donnée de taille n, il s'agit de maximiser la somme de n éléments pris parmi les n² éléments de la matrice avec pour contrainte de prendre exactement un élément pas ligne et par colonne. Nous sommes d'accord ?

Voici l'algorithme que je te propose. J'ignore s'il est optimal, il est en . C'est un algorithme récursif.

On note . (C'est bien le nombre que tu cherches.)

Pour M matrice de taille n et pour , on note 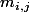la matrice de taille n-1 obtenue en enlevant la i-ième ligne et la j-ième colonne de M, et on note a_{i,j} le coefficient de M d'indice (i,j).

On a alors .

[Christophe Genolini]

Pour une matrice donnée de taille n, il s'agit de maximiser la somme de n éléments pris parmi les n² éléments de la matrice avec pour contrainte de prendre exactement un élément pas ligne et par colonne. Nous sommes d'accord ?

Oui

Voici l'algorithme que je te propose. J'ignore s'il est optimal, il est en . C'est un algorithme récursif.

En ?

Pour M matrice de taille n et pour , on note la matrice de taille n-1 obtenue en enlevant la i-ième ligne et la j-ième colonne de M, et on note a_{i,j} le coefficient de M d'indice (i,j).

Il y a donc coefficients a_{ij} possibles, pour chacun d'entre eux, il faut calculer ... J'ai plutot l'impression d'une complexite en . Ou alors, j'ai mal compris ta solution...

[Lierre Aeripz]

Il y a donc coefficients a_{ij} possibles, pour chacun d'entre eux, il faut calculer ... J'ai plutot l'impression d'une complexite en . Ou alors, j'ai mal compris ta solution...

En postant le message, je me disais bien que c'était étrange... Mais j'avais repoussé la réflexion à plus tard. J'ai confondu et dans le calcul :triste:...
Désolé pour l'inutilité de mon message...

[abcd22]

Bonsoir,
On pourrait commencer par ranger tous les éléments de la matrice dans l'ordre décroissant (en choisissant une structure de données où on peut enregistrer pour chaque élément la place initiale dans la matrice et la valeur), ensuite :
- on prend le plus grand élément et on place la colonne à laquelle il appartient de façon à ce qu'il soit sur la diagonale,
- on regarde le 2e élément et s'il n'est pas dans la colonne déjà placée et que son numéro de ligne ne correspond pas à une des colonnes déjà placée on place sa colonne pour que cet élément soit sur la diagonale
- ainsi de suite pour les éléments suivants.
Pour ordonner N éléments les meilleurs algorithmes sont en O(N log N) donc ça fait du O(n²log n) ici, et ensuite on parcourt n² éléments, on doit faire des vérifications d'indices avec au plus n-1 éléments à chaque fois, ça fait du O(n³) comme complexité au pire. Avec une méthode de tri naïve on a du O(N²), ça donnerait du O(n^4) comme complexité, c'est peut-être suffisant ici.
Il faut aussi justifier qu'on obtient bien la plus grande trace possible.

[Lierre Aeripz]

J'avais également pensé à cela, mais ça ne donne pas toujours le maximum.
Contre-exemple : .

On peut raffiner un peu en prenant le plus grand de la liste mais aussi voir ce que cela donne lorsque l'on prend le second voire le troisième. On se rapporche un peu plus du résultat...