Bonjour, j'ai un petit problème à résoudre..
En lançant deux dés, est il plus probable d'obtenir 8 et 6 avant deux 7 ?
Dans le premier cas on peut obtenir le 6 avant le 8 ou le 8 avant le 6.
Merci d'avance
Probabilité - dénonbrement
7 messages
- Page 1 sur 1
Bonsoir donc en lancant deux dés tu peu avoir les combinaisons suivantes :
11-12-13-14-15-16-21-22-23-24-25-26-31-32-33-34-35-36-41-42-43-44-45-46
-51-52-53-54-55-56-61-62-63-64-65-66
la sommes des 2 dés et donc :
2-3-4-5-6-7-3-4-5-6-7-8-4-5-6-7-8-9-5-6-7-8-9-10-6-7-8-9-
10-11-7-8-9-10-11-12
P(6et8)=5/36
P(7et7)=3/36
N'y a til pas un problème dans l'énoncé ? car d'apré mon raisonement on prendrais en compte 2 lancé de dés :hein:
11-12-13-14-15-16-21-22-23-24-25-26-31-32-33-34-35-36-41-42-43-44-45-46
-51-52-53-54-55-56-61-62-63-64-65-66
la sommes des 2 dés et donc :
2-3-4-5-6-7-3-4-5-6-7-8-4-5-6-7-8-9-5-6-7-8-9-10-6-7-8-9-
10-11-7-8-9-10-11-12
P(6et8)=5/36
P(7et7)=3/36
N'y a til pas un problème dans l'énoncé ? car d'apré mon raisonement on prendrais en compte 2 lancé de dés :hein:
non ce n'est pas sa pck ya aussi les coups 21 31 41 51 61 32 42 ...
En plus il faut perndre en compte que la premiere fois on peut obtenir soit un 8 soit un 6 et la seconde que le 8 ou que le 6.
La probabilité d'obtenir un 6 est de 5/36
La probabilité d'obtenir un 8 est de 5/36
La probabilité d'obtenir un 7 est de 6/36
Je sais aussi que l'on doit obtenir que la probabilité d'obtenir un 6 et un 8 avant deux 7 est de 0.546 mais je ne sais pas pourquoi...
En plus il faut perndre en compte que la premiere fois on peut obtenir soit un 8 soit un 6 et la seconde que le 8 ou que le 6.
La probabilité d'obtenir un 6 est de 5/36
La probabilité d'obtenir un 8 est de 5/36
La probabilité d'obtenir un 7 est de 6/36
Je sais aussi que l'on doit obtenir que la probabilité d'obtenir un 6 et un 8 avant deux 7 est de 0.546 mais je ne sais pas pourquoi...
Bonjour
En lançant deux dés, on va obtenir obtenir une paire. La proba que cette paire soit 6,8 est de 2/36 alors que la proba d'obtenir 7,7 est de 1/36.
Mais quand tu dis "proba d'obtenir 6,8 avant 7,7", cela veut dire que tu relances tes dés plusieurs fois. Dans ce cas, est-ce que tu conserves tes résulats ?
par exemple si tu obtiens 4,8 est-ce que tu gardes le 8 et tu relance un seul dé ?
Si tu te contentes de relancer tes dés jusqu'à obtenir soit (7,7) soit (6,8), les probas sont respectivement 1/3 et 2/3
En lançant deux dés, on va obtenir obtenir une paire. La proba que cette paire soit 6,8 est de 2/36 alors que la proba d'obtenir 7,7 est de 1/36.
Mais quand tu dis "proba d'obtenir 6,8 avant 7,7", cela veut dire que tu relances tes dés plusieurs fois. Dans ce cas, est-ce que tu conserves tes résulats ?
par exemple si tu obtiens 4,8 est-ce que tu gardes le 8 et tu relance un seul dé ?
Si tu te contentes de relancer tes dés jusqu'à obtenir soit (7,7) soit (6,8), les probas sont respectivement 1/3 et 2/3
Bonjour,
C'est un peu confus. Il te faut préciser. On lance 2 dés et on s'intéresse à la somme. et on recommence jusqu'à ce que les résultats aient donné soit deux fois une somme égale à 7 soit une somme égale à 6 et une somme égale à 8.
L'ordre d'apparition des sommes n'a pas d'importance.
Dans ce cas, la proba d'obtenir 6 et 8 avant deux 7 est bien de 0.546
On peut calculer la proba de d'obtenir un deuxiième 7 au (n+1)ième coup sans avoir sorti de 8,6 avant
Pour cela il faut qu'au nième coup, on ait déjà un total de 7 et soit
-pas de 6 ni de 8 -> P1
-que des 6 mais pas de 8->P2
-que des 8 mais pas de 6->P3
On a par symétrie P2=P3
notons p= prob d'obtenir 7, q= proba d'obtenir 8=prob obtenir 6, r=prob obtenir ni 6 ni 7 ni 8.
avec p+r+2q=1.
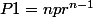 et
et 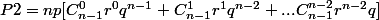
ou encore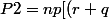^{n-1}-r^{n-1}])
et finalement la proba d'obtenir un double 7 avant au coup n+1 sera donnée par=p(P_1+2P_2)=np^2[2(r+q)^{n-1}-r^{n-1}])
Il suffit de sommer cette expression de n=1 à l'infini et ça donne
)^2}-\frac{p^2}{(1-r)^2})
La proba d'obtenir 6,8 avant est bien entendu le complémentaire
C'est un peu confus. Il te faut préciser. On lance 2 dés et on s'intéresse à la somme. et on recommence jusqu'à ce que les résultats aient donné soit deux fois une somme égale à 7 soit une somme égale à 6 et une somme égale à 8.
L'ordre d'apparition des sommes n'a pas d'importance.
Dans ce cas, la proba d'obtenir 6 et 8 avant deux 7 est bien de 0.546
On peut calculer la proba de d'obtenir un deuxiième 7 au (n+1)ième coup sans avoir sorti de 8,6 avant
Pour cela il faut qu'au nième coup, on ait déjà un total de 7 et soit
-pas de 6 ni de 8 -> P1
-que des 6 mais pas de 8->P2
-que des 8 mais pas de 6->P3
On a par symétrie P2=P3
notons p= prob d'obtenir 7, q= proba d'obtenir 8=prob obtenir 6, r=prob obtenir ni 6 ni 7 ni 8.
avec p+r+2q=1.
ou encore
et finalement la proba d'obtenir un double 7 avant au coup n+1 sera donnée par
Il suffit de sommer cette expression de n=1 à l'infini et ça donne
La proba d'obtenir 6,8 avant est bien entendu le complémentaire
Johnny001 a écrit:J'ai compris le début mais pas ce que j'ai cité, pouvez vous me l'expliquer?
P1+P2+P3 représente la proba d'être en situation favorable, en multipliant par p on a donc la proba que la paire de totaux égaux à 7 se réalise bien.
Donc la proba que le double 7 se réalisé d'abord est égale à celle qu'il se réalise au 2ième+au troisième...
Quant à la sommation, c'est un classique : on pose
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
