Suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
anemelie1
- Membre Naturel
- Messages: 92
- Enregistré le: 23 Oct 2005, 12:05
-
 par anemelie1 » 19 Avr 2007, 16:03
par anemelie1 » 19 Avr 2007, 16:03
je voulais savoir ce que sa voulait dire la question suivante:
etablir la relation U(n+1)-Un=((1-Un)(Un+2))/Un+4
d'apres moi sa veut dire de montrer l'égalité est ce que c'est sa?
-
Matthy
- Membre Naturel
- Messages: 64
- Enregistré le: 04 Jan 2006, 01:05
-
 par Matthy » 19 Avr 2007, 16:04
par Matthy » 19 Avr 2007, 16:04
Oui, c'est ca!
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 19 Avr 2007, 16:05
par allomomo » 19 Avr 2007, 16:05
Salut,
Un peu de respect pour les gens qui prennent de leur temps pour aider les autres ...
établir = c'est montrer que c'est ça ...
-
anemelie1
- Membre Naturel
- Messages: 92
- Enregistré le: 23 Oct 2005, 12:05
-
 par anemelie1 » 19 Avr 2007, 16:18
par anemelie1 » 19 Avr 2007, 16:18
je sais que ce quotient est plus grand que 0 et donc que Un est croissant mais je ne vois pas comment le justifié. pouvez vous me mettre sur la piste svp
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 19 Avr 2007, 16:56
par izamane95 » 19 Avr 2007, 16:56
salut anemelie 1
j'aimerai bien t'aider mais il faut que tu donne l'expression de Un
-
anemelie1
- Membre Naturel
- Messages: 92
- Enregistré le: 23 Oct 2005, 12:05
-
 par anemelie1 » 19 Avr 2007, 17:04
par anemelie1 » 19 Avr 2007, 17:04
U(n+1)=(3Un+2)/(Un+4)
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 19 Avr 2007, 17:12
par izamane95 » 19 Avr 2007, 17:12
ok
] - Un)
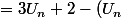^{2}-4U_{n}/(U_{n}+4))
=
^{2}/(U_{n}+4))
(U_{n}+2)/(U_{n}+4))
1 et 2 sont des racines de -Un+2-(Un)²
-
anemelie1
- Membre Naturel
- Messages: 92
- Enregistré le: 23 Oct 2005, 12:05
-
 par anemelie1 » 20 Avr 2007, 15:50
par anemelie1 » 20 Avr 2007, 15:50
Dans la suite de mon exercice on me demande de demontrer que la suite (Un) est convergente sachant que lintervalle est [0;1]
j'ai etudier les limites de 0 et de 1 avec U(n+1) mais je ne peut pas conclure qu'elle est convergente puisque je trouve 1/2 et 1
quelqu'un peut m'aider svp merci d'avance
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 20 Avr 2007, 21:18
par izamane95 » 20 Avr 2007, 21:18
pour démontrer qu' une suite est convergente il s'uffit de démontrer qu'elle est : soit croissante et majorée ou décroissante et minorée
dans notre cas on a
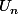
appartient à [0;1] donc

et

donc

donc
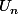
est croissante
résumons
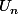
est croissante et majorée donc elle est convergente.
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
