4 Ensembles

[Dally]

Soient 4 ensembles E, E', F et F'

comment montrer que

et que penser de l'inclusion réciproque ?

[tize]

inclusion OK
inclusion réciproque fausse, par exemple si les 4 ensembles sont bien distincts, on peut avoir
et pourtant et

[sandrine_guillerme]

Bonsoir ,
bon pour l'inclusion réciproque c'est deja repondu par tize :)
et peut etre qu'il a pas fais attention pour l'autre allez je le post quand meme
tu consider un couple (x,y) dans ExF U E'xF' ça veut dire que (x,y) est dans ExF ou (x,y) est dans E'xF' ceci implique que x est dans E ou x est dans E' et y est dans F ou y est dans F' .. on obtient donc x est dans E U F' et y est dans F,F'
D'ou ce que tu cherchais
Bon courage .

[Moadib]

Je voudrais savoir comment fait-on pour insérer les symbôles mathématiques notamment ceux utilisés dans le cours des ensembles (inclusion, implication, etc) et merci.

[sandrine_guillerme]

Bonjour ,

Je ne comprends pas ta question ..

tu veux dire comment écrire en Latex si c'est ça .. voici un lien ..

Bon courage .

[Moadib]

C'est ça, Sendrine, merci.

Alors, peux-tu m'aider à résoudre les 2 exercices suivants:

1 - P désigne une partition d'un ensemble non vide E. La relation : "x\inE, y\inE, x et y appartiennent à un même élément P" est-elle réflexive ?

2 - Soit un ensemble A non vide et E=\mathcal{P(A)}, la relation : "B\inE, D\inE et B\capD=\empty" est-elle réflexive ?

Salutations

[sandrine_guillerme]

C'est ça, Sandrine, merci.

Alors, peux-tu m'aider à résoudre les 2 exercices suivants:

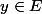
1 - P désigne une partition d'un ensemble non vide E. La relation : ", , x et y appartiennent à un même élément P" est-elle réflexive ?

2 - Soit un ensemble A non vide et , la relation : "" est-elle réflexive ?

Salutations

C'est ce que tu voulais écrire, il faut venir au début de la formule tape : il faut rajouter la balise tex au début et à la fin (pour mieux voir comment j'ai fais clique sur citer en bas a droite de mon message .

[sandrine_guillerme]

désolée pour l'exo j'ai cours mais il y a ceux qui peuvent t'aider;;

je fais appel a rain fahr ou serge svp?

[Moadib]

Merci pour l'aide. A bientôt Sandrine.

[fahr451]

bonjour

tu as cherché ?

[Moadib]

Bonjour Fahr,

Oui, mais j'ai pas trouvé. Pourtant ça doit crever les yeux :cry:

[fahr451]

pour la première si on fait x = y "ça marche" ou pas ?
pour la deuxième si on fait B = D = A ?

[Moadib]

Pour la première que penses-tu de la solution suivante:

Si et seulement si xRx et yRy appartiennent à la diagonale du Graphe de la relation et que la partie de P à laquelle appartiennent x et y est justement faite des éléments qui sont en relation avec eux-mêmes. Ou est ce une tautologie ce que je viens de dire ?


Pour la deuxième, si on pose B=D=A alors BD .

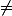
J'attend tes commentaires.

Cordialement.

[Moadib]

Fahr, je n'arrive plus à aller sur la page 2, je reçois le message suivant:

Impossible d'ajouter les cookies, les en-têtes ont déjà été envoyés.
Fichier : /home/maths/www/includes/functions_mimetex.php
Ligne : 48

Peux-tu me dire comment y remédier ? merci

[Moadib]

Je propose ce qui suit pour la deuxième:

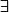
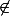
B D= , donc x B et x D. Or si x est en relation avec lui même et il ne fait pas partie de D, cela revient à dire que la relation n'est pas réflexive.

Que penses-tu ?

[fahr451]

j ai eu le même problème que toi
ne va pas nous faire sauter le forum!


la deuxième n 'est pas réflexive car A n 'est pas en relation avec A

la première je ne suis pas sûr de bien comprendre

P est une partition

xR y ssi x et y appartiennent à une même classe( partie) de la partition
c'est ce que j'ai compris
x et x sont dans la même classe donc R est réflexive

[Moadib]

Pour que la relation soit réflexive, il faut que tous les éléments de l'ensemble soient en relation avec eux-mêmes.

x et y doivent être en relation avec eux mêmes. Et, s'ils appartiennent à une classe et qu'on ne considère la réflexivité que dans les limites de cette classe, cette relation ne peut être réflexive que si tous ses éléments sont en relation avec eux memes, Donc, cette classe ne contient que ces deux éléments si la relation ambitionne d'être réflexive. En d'autres termes et comme tu l'as explicité plus haut : xRx et x=y.

Si la réflexivité s'applique à tout l'ensemble E, alors la classe dont il est question est justement la diagonale du graphe.

Cordialement