Un défi complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mathelot
 par mathelot » 24 Mar 2007, 13:50
par mathelot » 24 Mar 2007, 13:50
bonjour,
saurez-vous relever ce nouveau défi ?
Soit le nombre complexe

.
calculer

(chaque exposant est lui-même une puissance)
-
pimboli4212
- Membre Relatif
- Messages: 164
- Enregistré le: 02 Nov 2006, 10:38
-
 par pimboli4212 » 24 Mar 2007, 14:22
par pimboli4212 » 24 Mar 2007, 14:22
Bonjour
Juste une petite question : c'est normal de prendre peur en voyant ça ? ^^
edit: du latex ? ^^
Sinon mouais mandriva ... je viens de cette communauté à la base mais j'ai switcher pour ubuntu pour plusieur raison [philosophie, gnome's powaaa ^^, acceuil de la communauté, ...]
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Mar 2007, 14:28
par Flodelarab » 24 Mar 2007, 14:28
Nonnnn c que du LaTex...

non?
ps: je suis sous mandriva et c de la balle.
-
clems
- Messages: 3
- Enregistré le: 24 Mar 2007, 14:34
-
 par clems » 24 Mar 2007, 14:49
par clems » 24 Mar 2007, 14:49
Peut-être faut-il utiliser la méthode de ...Moivre je crois?
Ce qui donnerai :

=cos(2006x2007x2008x

/3)+i(sin (2006x2007x2008x

/3) soit environ 0.538526242 + i (0.8426087388).
Je ne suis pas sûr de moi du tout !!!
-
Blueberry
- Membre Relatif
- Messages: 243
- Enregistré le: 04 Mar 2007, 09:51
-
 par Blueberry » 24 Mar 2007, 14:55
par Blueberry » 24 Mar 2007, 14:55
Bonjour,
il me semble que les puissances de cette exponentielle complexe donnent périodiquement les mêmes valeurs, non ?
-
clems
- Messages: 3
- Enregistré le: 24 Mar 2007, 14:34
-
 par clems » 24 Mar 2007, 14:58
par clems » 24 Mar 2007, 14:58
Oui c'est pour cela que (e^pi/3)^n=cos(n.pi/3)+i(sin(n.pi/3)) :hein:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Mar 2007, 14:58
par Flodelarab » 24 Mar 2007, 14:58
clems a écrit:Peut-être feut-il utiliser la méthode de ...Moivre je crois?
Ce qui donnerai :

=cos(2006x2007x2008x

/3)+i(sin (2006x2007x2008x

/3) soit environ 0.538526242 + i (0.8426087388).
Je ne suis pas sûr de moi du tout !!!
Ce que tu n'as pas saisi c'est que toi tu réponds à ça:
^{2006}\)^{2007}\)^{2008})
alors que c ça:

-
clems
- Messages: 3
- Enregistré le: 24 Mar 2007, 14:34
-
 par clems » 24 Mar 2007, 14:59
par clems » 24 Mar 2007, 14:59
Ah oki !!!
-
mathelot
 par mathelot » 24 Mar 2007, 16:54
par mathelot » 24 Mar 2007, 16:54
Blueberry a écrit:Bonjour,
il me semble que les puissances de cette exponentielle complexe donnent périodiquement les mêmes valeurs, non ?
super ! :++: donc on va traiter l'entier

, modulo quoi ?? (ou, pour quelles valeurs n, l'exposant n donne

)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Mar 2007, 17:26
par Flodelarab » 24 Mar 2007, 17:26
Au point ou en est le sujet de discussion, j'étaie ma réponse
exp(iPi/3) est une rotation de centre O et d'angle Pi/3
Donc comme on fait un tour chaque fois qu'on a appliquer 6 fois la rotation on va chercher modulo 6
or 2006= 2004+2=6*334 + 2
Quelque soit l'exposant, un seul terme survivra au modulo: 2^(2007^2008)
Mais si on fait des groupes de 3, on reviendra au point de départ (car 2*3=6)
or 2007 est multiple de 3
Donc on reviendra forcément au point de départ.
SAUF que je me suis trompé. Car le point de départ n'est pas oméga comme je l'ai marqué dans le précédent post, mais 1.
La réponse est donc 1
-
mathelot
 par mathelot » 24 Mar 2007, 17:37
par mathelot » 24 Mar 2007, 17:37
Flodelarab a écrit:Au point ou en est le sujet de discussion, j'étaie ma réponse
exp(iPi/3) est une rotation de centre O et d'angle Pi/3
Donc comme on fait un tour chaque fois qu'on a appliquer 6 fois la rotation on va chercher modulo 6
or 2006= 2004+2=6*334 + 2
Quelque soit l'exposant, un seul terme survivra au modulo: 2^(2007^2008)
On peut donc remplacer l'exposant

par l'exposant

car on peut faire des produits de moduli , donc aussi des puissances...
peut être, on pourrait regarder les premières puissances de 2:

modulo 6 ..
Flodelarab a écrit:La réponse est donc 1
ce n'est pas exact, mais on est sur la bonne voie...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Mar 2007, 18:38
par Flodelarab » 24 Mar 2007, 18:38
Ah oui! Double faute.
Le coup des groupes de 3 ça marche absolument pas.
c soit 2 soit 4
or 2007^2008 est impair donc c 2
Il reste
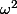
soit

Je les aurais tous fait :ptdr:
-
mathelot
 par mathelot » 24 Mar 2007, 18:58
par mathelot » 24 Mar 2007, 18:58
Bravo, Flodelarab. On trouve

comme résultat. :++:
En effet, si on regarde l'exposant de

en tant que puissance de 2, on trouve modulo 6:
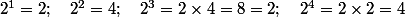
..
donc:
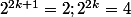
modulo 6.
Comme

est impair, nous avons l'égalité, modulo 6:

le résultat est donc:
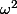
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités