Probleme d'aire et de fonction

[coco0610]

bonjour, j'ai un exercice que je n'ai pas très bien compris pouvez-vs m'aidez svp :

ABC est un triangle isocèle en A avec :
AB=AC=10 cm
H est ke pied de la hauteur issue de A.

On se propose d'étudier les variations de l'aire du triangle lorsqu'on fait varier la longueur x ( en cm ) du côté [BC]

A.DECOUVERTE D'UNE FONCTION
1.a) Calculer la valeur exacte de l'aire de ABC lorque x=5, puis lorsque x=10
[ Donc j'ai d'abord calculer la hauteur du triangle, j'ai trouver la valeur exacte qui est : ;)95 puis j'ai appliqué la formule : Base*Hauteur/2 : j'ai trouvé : 24.36 mais ce n'est pas l'aire exacte c'est un arrondi puis pour x=5 j'ai trouvé : 48.73 ]

1.b) Peut-on avoir x=30 ? pourquoi ? Dans quel intervalle varie x ?
[j'ai répondu : Non,on ne peut pas avoir x=30 car si la hauteur est toujours la même, les côtés [AC] et [AB] ne mesureront plus 10 cm mais plus. ]

2.a) Exprimer AH en fonction de x.
[ Alors là je ne sais pas si c'est une fonction qu'il faut répondre ou un graphique ]

2.b) On désigne f(x) l'aire ABC.
Démontrer que : f(x)=x/4;)400-x². ( la racine carrée s'arrete jusque x²)
[ Cette question là, je n'y arrive pas ]

Voici une partie de mon exercice pouvez-vous m'aider svp
Merci d'avance.

[armor92]

Bonjour coco,

1.a)
L'aire du triangle est donnée par la formule : x * AH / 2
Le problême est de calculer AH en fonction de x.

On applique pythagore dans le triangle rectangle ABH :
AB² = AH² + BH²
AB = 10 et BH = x/2
AH² = 100 - (x/2)² = 100 - x²/4

Si x = 5, AH² = 100 - 25/4 = 375/4
AH = =
Aire = =
Si x = 10, AH² = 100 - 100/4 = 75
AH = =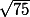
Aire = =

1.b) On ne peut pas avoir x= 30 car BC <= AB+ AC.
BC = 20 au maximum
x varie dans l'intervalle [0;20]

[armor92]

2.a)
On a montré dans le 1.a) que :
AH² = 100 - x²/4
Donc AH =

2.b)
Aire = f(x) = x * AH / 2 = = =

[coco0610]

Merci sincèrement de m'avoir aidé car je viens de m'apercevoir que je n'avais pas du tout réussi cet exercice.
Merci :++:

[coco0610]

Quelles sOnt les étapes intermédiaires entre :
AH =;)375/4
AH = 5/2;)15

Merci d'avance .

[armor92]

= = = =

[coco0610]

Merci beaucOup.

Calculer f(x) pour chacune des valeurs entières de x prise dans [0;20], arrOndir les résultats au dixième et les présenter dans un tableau.
J'ai remplis un tableau.
Puis j'ai fait une cOurbe.

[ vOici la suite de l'exercice ]

B.Recherche de l'aire maximale
La fonction f admet un maximum pour une valeur x0 de x.

1a) Encadrer x0 par deux entiers consécutifs.
b) Recopier et compléter le tableau suivant :

[x] [14.1][14.11][14.12][14.13][14.14][14.15][14.16]
[f(x)][...] [...] [...] [...] [...] [...] [...]

Donnez un encadrement "plus fin" de x0.

2. On note K le pied de la hauteur ABC issue de B.
a) Démontrer que l'aire de ABC est égale a 5BK.
b) Quelle est la nature du triangle ABC lorque la longueur BK est maximale ?
c) En déduire la valeur exacte de x0.

Merci d'avance.

[armor92]

B.
1)
a) Pour la recherche de l'aire maximale, on doit évaluer f(x) pour x entier de 0 à 20
x=13 f(x)=49.3957
x=14 f(x)=49.9900
x=15 f(x)=49.6078
Le maximum x0 est atteint entre 14 et 15

b)
x=14.11 f(x)=49.99948482
x=14.12 f(x)=49.99975539
x=14.13 f(x)=49.99992643
x=14.14 f(x)=49.99999772
x=14.15 f(x)=49.99996906
On peut donner un encadrement plus fin de x0
14.14 <= x0 <= 14.15

[armor92]

2)
a) L'aire d'un triangle est égale à base * hauteur /2
Ici on prend pour base AC = 10
La hauteur associée à cette base est BK
Donc aire = BK * 10 / 2 = BK * 5

b) On voit que la hauteur BK est maximale lorsque le triangle ABC est rectangle en A.

c) On alors x0 = BC
Théoreme de pythagore : BC² = AB² + AC² = 100 + 100 = 200
Donc x0 = BC = =

[coco0610]

Merci c'est très gentil !

J'aurai encOre quelque chOse à vOus demander :

Est ce que je pOurrez avOir la valeur du tableau pour :
x=14.1 et x=14.16
Merci d'avance !

[armor92]

Pour :
x=14.1 f(x)=49.99911493
x=14.16 f(x)=49.99984023
Cordialement