Fonction dérivée

par **didine_2001** » 12 Fév 2007, 20:29

bonjour, j'ai un article avec des formule qui sont données et j'essaie de voir comment c'est formule sont obtenues.
j'ai une longueur l = racine carrée de a²+b²+cos(x), ça j'ai trouvé comment ils ont fait.
Ensuite avec ça il calcule une vitesse, je sais qu'il faut dérivée mais je n'arrive pas à leur résultat: le résultat est x' absin(x) / l

NB: Ceci à partir d'un triangle quelconque avec comme côté a, b et l est l'angle x situé entre b et l.

Merci d'avance pour votre aide

par **mathelot** » 12 Fév 2007, 21:00

bonjour,
je te propose la relation d'Al-kashi:
si ab,l sont les côtés du triangle et l est le côté opposé à l'angle x:

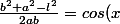d'où:

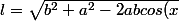en dérivant l par rapport à 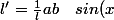x:

et on obtient la formule demandée.

par **didine_2001** » 13 Fév 2007, 16:28

merci beaucoup, ça m'aide bien car je ne me suis plus servie des dérivées depuis déja longtemps et ça me parait trés loin.
J'aurai peut être encore besoin d'aide plus tard

par **didine_2001** » 13 Fév 2007, 18:51

Pourriez vous me confirmer s'il vous plait que la dérivée de " l' " est:
l'' = (x''.l ) / absin(x)

Merci d'avance

par **mathelot** » 13 Fév 2007, 19:32

euh, ça a l'air faux :bad:

par **didine_2001** » 13 Fév 2007, 21:33

c'est pourtant l'équation que j'ai dans mon article, quel serait le résultat d'après vous

par **mathelot** » 14 Fév 2007, 10:43

tu peux scanner l'article ?

par **didine_2001** » 14 Fév 2007, 13:00

voila je l'ai scanné. Mais comment vous le faire parvenir ? Je ne peux pas joindre de fichiers.

Fonction dérivée

fonction dérivée

Qui est en ligne