Bonjour.
J'arrive à écrire
10^5 =
10000 =
120 + 5*9^5 - 10*8^5 + 10*7^5 - 5*6^5 + 5^5
en me servant d'une représentation triangulaire particulière que je m'attribue :
0 1
1 1 1
2 2 2 -1
3 6 3 -3 1
4 24 4 -6 4 -1
5 120 5 -10 10 -5 1
Je n'ai toujours pas trouvé une telle présentation qui serait antérieure à la mienne.
Si vous avez des renseignements sur un tel résultat merci de le noter sur le présent forum.
équations avec des puissances de nombres
9 messages
- Page 1 sur 1
Re: équations avec des puissances de nombres
Bonjour ;
Peux-tu expliciter ce que donne l'avant dernière ligne de la représentation triangulaire ?
Peux-tu expliciter ce que donne l'avant dernière ligne de la représentation triangulaire ?
Re: équations avec des puissances de nombres
Ça m'étonnerait que l'identité
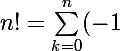^k\, \binom{n}{k}\, (x-k)^n)
ne soit pas déjà écrite quelque part.
ne soit pas déjà écrite quelque part.
 Re: équations avec des puissances de nombres
Re: équations avec des puissances de nombres
Merci à tous pour l'aide.
Je n'ai rien inventé !
Il me faut voir du côté de la machine de Babbage et du théorème :
La différence d'ordre n des nombres successifs élevés à la puissance n est constante. Cette constante est égale à n! (factorielle n)
Ça marche pour tout nombre x à la place des entiers successifs.
Je n'ai rien inventé !
Il me faut voir du côté de la machine de Babbage et du théorème :
La différence d'ordre n des nombres successifs élevés à la puissance n est constante. Cette constante est égale à n! (factorielle n)
Ça marche pour tout nombre x à la place des entiers successifs.
 Re: équations avec des puissances de nombres
Re: équations avec des puissances de nombres
Il s'agit de calculer la factorielle n! sous forme de somme :
n! = \prod_{k=1}^{n}{k}
= \sum_{k=0}^{n}{\left(-1\right)^k }\begin{pmatrix}
n
\\
k
\end{pmatrix}
(x-k)^n
= \sum_{k,l=0}^{n}{\left(-1\right)^{k+l}}\begin{pmatrix}
n
\\
k
\end{pmatrix}
\begin{pmatrix}
n
\\
l
\end{pmatrix}
x^{n-l} k^l
Il semble que Chat GPT lui-même écarte la possibilité d'une telle écriture sous forme directe de somme.
n! = \prod_{k=1}^{n}{k}
= \sum_{k=0}^{n}{\left(-1\right)^k }\begin{pmatrix}
n
\\
k
\end{pmatrix}
(x-k)^n
= \sum_{k,l=0}^{n}{\left(-1\right)^{k+l}}\begin{pmatrix}
n
\\
k
\end{pmatrix}
\begin{pmatrix}
n
\\
l
\end{pmatrix}
x^{n-l} k^l
Il semble que Chat GPT lui-même écarte la possibilité d'une telle écriture sous forme directe de somme.
Re: équations avec des puissances de nombres
LoPol a écrit:Il s'agit de calculer la factorielle n! sous forme de somme :
Il semble que Chat GPT lui-même écarte la possibilité d'une telle écriture sous forme directe de somme.
Re: équations avec des puissances de nombres
Bonjour,
C'est un cas particulier de la formule (10) ici : https://en.wikipedia.org/wiki/Binomial_coefficient#math_10
C'est un cas particulier de la formule (10) ici : https://en.wikipedia.org/wiki/Binomial_coefficient#math_10
Re: équations avec des puissances de nombres
Bravo !
Ce n'est pas aujourd'hui que j'ai réinventer l'eau chaude !
Ce n'est pas aujourd'hui que j'ai réinventer l'eau chaude !
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
