Bonjour,
Je vous prie de bien vouloir trouver ci-joint un exercice sur lequel je sèche et je souhaitais avoir vos avis quant à la réponse à apporter. J'ai trouvé les dérivées par rapport à x et à y puis je ne vois pas bien comment résoudre le système pour faire une disjonction de cas afin de trouver alpha et beta. Merci d'avance.
En fonction des paramètres (α,β) ∈]1,+∞[2, déterminer les points critiques et étudier la nature des extrémas locaux de la fonction définie pour tout (x, y) ∈ R2 par f(x, y) = x^2/(α^2 − 1) + 2xy/(αβ − 1) + y^2/(β^2 − 1).
Fonction de deux variables
4 messages
- Page 1 sur 1
Re: Fonction de deux variables
Salut,
Personne ne te demande de "trouver et
et  ", on te demande de trouver les points critique (et leur nature) en fonction de
", on te demande de trouver les points critique (et leur nature) en fonction de  et
et  (*).
(*).
Et, pour déterminer les points critiques, ben tu as un gentil système linéaire de deux équations à deux inconnues (à savoir et
et  ) dans lequel
) dans lequel  et
et  sont des "paramètres", c'est à dire des valeurs considérées comme connues.
sont des "paramètres", c'est à dire des valeurs considérées comme connues.
Après, il risque effectivement d'y avoir des cas particulier (pour et
et  ) à traiter à part vu que dans ce cas, le système est dégénéré.
) à traiter à part vu que dans ce cas, le système est dégénéré.
(*) Tu ne fait pas de différence entre les question "que fera tu demain en fonction de la météo ?" et "trouve moi quelle sera la météo de demain ?" ?
Personne ne te demande de "trouver
Et, pour déterminer les points critiques, ben tu as un gentil système linéaire de deux équations à deux inconnues (à savoir
Après, il risque effectivement d'y avoir des cas particulier (pour
(*) Tu ne fait pas de différence entre les question "que fera tu demain en fonction de la météo ?" et "trouve moi quelle sera la météo de demain ?" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fonction de deux variables
Le soucis demeure la résolution de ce système. j'obtiens x=0 et y=0 mais rien de bien important, donc, concernant les paramètres.
Re: Fonction de deux variables
C'est effectivement l'unique solution dans le cas général, mais par contre le système est dégénéré (avec une infinité de solutions) dans le cas particulier où 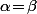 .
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
