Convergence uniforme

[fpaco]

Bonjour, petite question,

est ce que si une série de fonction converge uniformément sur tout intervalle fermé d'un ensemble, alors elle converge uniformément sur l'ensemble tout entier ?
je sais que pour le suites de fonction ce n'est pas le cas mais est-ce le cas pour les séries de fonction ? (mon petit doigt me dit que non mais je n'arrive pas a trouver de contre exemple)

Et j'ai la même question avec des intervalles ouverts

merci de votre aide

[GaBuZoMeu]

Bonsoir,

ta qustion n'est pas très claire : qu'est-ce que "intervalle fermé d'un ensemble", pour toi ? Pour moi, est un intervalle fermé de (et aussi un intervalle ouvert).
Tu veux peut-être dire compact (= fermé borné) ?

[fpaco]

Par exemple si somme(f_n) converge uniformément sur [-a;a] pour tout a appartenant a R alors somme(f_n) converge uniformément sur R.

Et si somme(f_n) converge uniformément sur ]-a;a[ pour tout a appartenant a R alors somme(f_n) converge uniformément sur R.

Est ce que ces 2 propositions sont vraies ?

[GaBuZoMeu]

Non, elles sont fausses.
Prends par exemple la série de l'exponentielle. Elle converge uniformément sur tout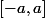 (et a fortiori sur tout 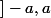, mais elle ne converge évidemment pas uniformément sur (pour tout polynôme , n'est pas borné sur ).
Mais la convergence uniforme sur tout compact suffit pour bon nombre de résultats : par exemple si une série entière converge uniformémément sur tout compact de , alors sa somme est bien et même nanalytique sur tout entier.

[tournesol]

0

[fpaco]

Mmmmm ok
merci de votre aide.