Suites récurrentes d'ordre 2

[ludo60]

Bonjour, je rencontre une difficulté pour comprendre une ligne dans un livre à propos de l'écriture des solutions d'une suite récurrente linéaire d'ordre 2.

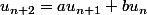
Soit donc une suite vérifiant la relation (E).
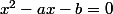
On note l'équation caractéristique associée qui admet une racine double .

Le but est de montrer que la suite vérifie (E).
Il est écrit: "Ici, on a " Je ne comprends pas d'où vient cette assertion. Je me doute qu'il s'agit d'une bricole mais je sèche complètement !
Merci pour votre aide

[mathelot]

bonjour,
r est une racine double, elle annule le trinôme mais aussi sa dérivée:








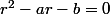
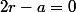
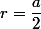
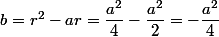
on développe et on remplace r par sa valeur.

[ludo60]

Merci ! Néanmoins, je pense que l'auteur raisonne autrement car il déduit justement de cette première égalité le fait que a=2r et que b=-r² par identification:

On a ici (x-r)²=x²-ax-b et donc, a=2r et b=-r²

[catamat]

Bonjour

Je pense que c'est la formule de factorisation d'un trinôme ayant une racine double x'
ax²+bx+c=a(x-x')²

ici a vaut 1 et x' vaut r

donc x²-ax-b=(x-r)²

[ludo60]

Bonjour, d'accord, ça doit tout simplement être cela. Merci pour le debug