Bonjour.
Je n'arrive jamais a comprendre une notion dans le contexte des differentielles. Comment considerons-nous les dx, dy, dz, qui pour moi sont des variations infiniment petites de x, y, z, comme une base pour l'espace des formes lineaires?
Si on prend R^2 par exemple. Une forme lineaire sur R^2 est f(x,y)=x+y.
Cette f peut elle vraiment etre exprimee en fonctions des dx et dy? Je comprends pas ce lien. F est une fonction, comment disons nous que les differentielles de x et y forment une base pour un espace de formes lineaires
Et comment ces dx et dy sont les projections des coordonnees des formes differentielles
Formes differentielles
5 messages
- Page 1 sur 1
Re: Formes differentielles
dx désigne , dans le contexte des formes différentielles , la fonction abscisse .
dy est la fonction ordonnée .
Utilisation non confuse : dx(h,k)=h , et dy(h,k)=k .
dx et dy sont donc des formes linéaires : ce sont les formes coordonnées .
Toute forme lineaire sur R2 a des images de la forme ah+bk .
Elle est donc combinaison linéaire des coordonnees . Elle est égale à adx+bdy .
Une forme differentielle sur R2 n'est pas une forme linéaire mais une fonction qui , à (x,y) fait correspondre une forme linéaire . C'est donc une fonction de R2 dans L1(R2)
Par exemple : la forme différentielle définie par D(x,y) =dx+(x^2+y)dy) peut être considérée comme une forme linéaire à coefficients variables .
peut être considérée comme une forme linéaire à coefficients variables .
On a : (D(x,y))(h,k)=+(x^2+y)dy(h,k)=2xyh+(x^2+y)k)
Cette forme est-elle exacte ?
dy est la fonction ordonnée .
Utilisation non confuse : dx(h,k)=h , et dy(h,k)=k .
dx et dy sont donc des formes linéaires : ce sont les formes coordonnées .
Toute forme lineaire sur R2 a des images de la forme ah+bk .
Elle est donc combinaison linéaire des coordonnees . Elle est égale à adx+bdy .
Une forme differentielle sur R2 n'est pas une forme linéaire mais une fonction qui , à (x,y) fait correspondre une forme linéaire . C'est donc une fonction de R2 dans L1(R2)
Par exemple : la forme différentielle définie par D(x,y) =
On a : (D(x,y))(h,k)=
Cette forme est-elle exacte ?
Re: Formes differentielles
Oui j'ai compris ca, mais ce que je ne comprrnds toujours pas c'est comment les dx et dy sont des formes coordonnees/une base. Si f: R^2->R s'ecrit f(h,k)=ah+bk, donc f= adx+bdy?? Dans la premiere c'est une application lineaire, dans la seconde cest une expression avec des differentielles
Re: Formes differentielles
Si t'as compris ça , relis et analyse ce que je t'ai expliqué ; tout est dedans .
Re: Formes differentielles
Par exemple, avec la sphère 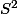 de centre O
de centre O
r est un réel strictement positif
x,y,z réels
Une équation de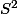 est
est 
on différentie:
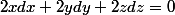
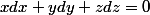 (*)
(*)
ici, au point M de la sphère de coordonnées (x,y,z), l'espace tangent est un plan affine, contenant M, et perpendiculaire au rayon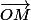 car (*) est interprété comme un produit scalaire.
car (*) est interprété comme un produit scalaire.
On peut tracer des courbes (paramètrées) sur la sphère. Ces courbes, au point M, ont un vecteur vitesse.
Ce vecteur vitesse instantanée appartient au plan tangent noté
Exemple:
soit la courbe d'équation cos(t^2),r cos(t) sin(t^2),r sin(t)))
on vérifie que le point N(t) appartient à la sphère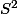 .
.
en différentiant:
cos(t^2)-cos(t)2t sin(t^2))dt)
sin(t^2)+cos(t)2t cos(t^2))dt)
 dt)
on vérifie par un calcul assez long mais ne présentant pas de difficulté que l'on a bien:
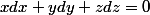
Ceci montre , sur un exemple,que les vecteurs vitesse instantanée des courbes tracées sur la sphère
sont des vecteurs du plan tangent. Mieux, l'espace tangent à la courbe, en un point M de la sphère, est une droite , incluse dans le plan tangent d'équation paramètrique de paramètre dt
r est un réel strictement positif
x,y,z réels
Une équation de
on différentie:
ici, au point M de la sphère de coordonnées (x,y,z), l'espace tangent est un plan affine, contenant M, et perpendiculaire au rayon
On peut tracer des courbes (paramètrées) sur la sphère. Ces courbes, au point M, ont un vecteur vitesse.
Ce vecteur vitesse instantanée appartient au plan tangent noté
Exemple:
soit la courbe d'équation
on vérifie que le point N(t) appartient à la sphère
en différentiant:
on vérifie par un calcul assez long mais ne présentant pas de difficulté que l'on a bien:
Ceci montre , sur un exemple,que les vecteurs vitesse instantanée des courbes tracées sur la sphère
sont des vecteurs du plan tangent. Mieux, l'espace tangent à la courbe, en un point M de la sphère, est une droite , incluse dans le plan tangent d'équation paramètrique de paramètre dt
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
