Matrices et formes linéaires

par **Supernova** » 15 Avr 2012, 13:01

Salut à tous!

je suis bloquée devant une question concernant la leçon des: Matrices et applications linéaires. la voici:
f une forme linéaire sur Mn(IK) tq pr tt (A,B)£(Mn(IK))^2, f(AB)=f(BA)
mq f(Eij)=0 et f(Ejj)=f(Eii) pour tt i,j£{1,2,.....,n} puis en déduire l'existence d'un µ tq f=µTr (Tr: trace)

Merci d'avance

par **Le_chat** » 15 Avr 2012, 13:13

Salut.

Si par exemple pour A et B tu prends les matrices Eij et Ekl pour i,j,k,l quelconques, ça devrait te donner les relations que tu cherches en choisissant à posteriori i,j,k et l.

par **Supernova** » 15 Avr 2012, 13:18

Des relations, peux-tu m'en donner une? :)

par **ev85** » 15 Avr 2012, 13:43

Supernova a écrit:Des relations, peux-tu m'en donner une?

Tu calcules le produit

dans le cas général puis

et

.

par **Supernova** » 15 Avr 2012, 17:04

D'acc !

Eij x Ekl = delta(jk) x Eil et Ekl x Eij = delta(li) x Ekj
Eij x Eii = 0 et Eii x Eii = Eii
c ça?

par **ev85** » 15 Avr 2012, 17:09

Supernova a écrit:D'acc !

Eij x Ekl = delta(jk) x Eil et Ekl x Eij = delta(li) x Ekj
Eij x Eii = 0 et Eii x Eii = Eii
c ça?

Oui, sauf que j'ai dérapé dans le

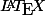
, je voulais dire

histoire que tu puisses répondre à la question de l'énoncé.

par **Supernova** » 15 Avr 2012, 22:09

ouais! Merci en tout cas

Matrices et formes linéaires

Matrices et formes linéaires

Qui est en ligne